Clayton Shonkwiler

Research

My work uses differential geometry to solve topological and physical problems. My main current interest is in applying techniques from Riemannian and symplectic geometry and geometric probability to polymer network models and to statistical signal processing. My research is partially supported by the National Science Foundation (DMS–2107700), and previously by the Simons Foundation (#354225 and #709150).

Publications

Note: when possible, each collaborator’s name is linked to their website (or the nearest approximation thereof). Click the thumbnails for a more detailed description. See also my arXiv author page and my Google Scholar profile.

  1. “Three proofs of the Benedetto–Fickus theorem”
    Joint with Dustin G. Mixon, Tom Needham, and Soledad Villar
    Stephen D. Casey, M. Maurice Dodson, Paulo J.S.G. Ferreira, Ahmed Zayed, editors, Sampling, Approximation, and Signal Analysis: Harmonic Analysis in the Spirit of J. Rowland Higgins, Applied and Numerical Harmonic Analysis, Birkhäuser, Cham, 2023, 371–391 (chapter link)
    doi: 10.1007/978–3–031–41130–4_14; arXiv: 2112.02916 [math.MG]

  2. “Fusion frame homotopy and tightening fusion frames by gradient descent”
    Joint with Tom Needham
    Journal of Fourier Analysis and Applications 29 (2023), no. 4, 51 (journal link)
    MR: 4621029; Zbl: 07727373; doi: 10.1007/s00041–023–10028–0; arXiv: 2208.11045 [math.FA]

  3. “Robocasting of ceramic Fischer–Koch S scaffolds for bone tissue engineering”
    Joint with Vail Baumer, Erin Gunn, Valerie Riegle, Claire Bailey, and David Prawel
    Journal of Functional Biomaterials 14 (2023), no. 5, 251 (journal link)
    Selected as an Editor’s Choice
    PMID: 37233361; doi: 10.3390/jfb14050251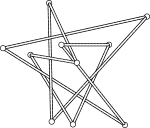

  4. 10-stick 10_16 knot “New stick number bounds from random sampling of confined polygons”
    Joint with Thomas D. Eddy
    Experimental Mathematics 31 (2022), no. 4, 1373–1395 (journal link)
    Special Issue on Illustration and Visualization in Mathematics Research
    stick-knot-gen has supporting code and data, including bounds on stick number for knots through 10 crossings
    MR: 4516264; Zbl: 07628940; doi: 10.1080/10586458.2021.1926000; arXiv: 1909.00917 [math.GT]

  5. “Radius of gyration, contraction factors, and subdivisions of topological polymers”
    Joint with Jason Cantarella, Tetsuo Deguchi, and Erica Uehara
    Journal of Physics A: Mathematical and Theoretical 55 (2022), no. 47, 475202 (journal link)
    MR: 4516726; doi: 10.1088/1751–8121/aca300; arXiv: 2004.06199 [cond-mat.stat-mech]

  6. “New superbridge index calculations from non-minimal realizations”
    Journal of Knot Theory and Its Ramifications 31 (2022), no. 10, 2250063 (journal link)
    stick-knot-gen has supporting code and data, including bounds on superbridge index for knots through 10 crossings
    MR: 4496244; Zbl: 1504.57012; doi: 10.1142/S0218216522500638; arXiv: 2206.06950 [math.GT]

  7. “Toric symplectic geometry and full spark frames”
    Joint with Tom Needham
    Applied and Computational Harmonic Analysis 61 (2022), 254–287 (journal link)
    MR: 4456799; Zbl: 1496.42041; doi: 10.1016/j.acha.2022.07.004; arXiv: 2110.11295 [math.FA]

  8. “All prime knots through 10 crossings have superbridge index ≤ 5”
    Journal of Knot Theory and Its Ramifications 31 (2022), no. 4, 2250023 (journal link)
    stick-knot-gen has supporting code and data, including bounds on stick number and superbridge index for knots through 10 crossings
    MR: 4445215; Zbl: 1494.57011; doi: 10.1142/S0218216522500237; arXiv: 2112.10902 [math.GT]

  9. “Admissibility and frame homotopy for quaternionic frames”
    Joint with Tom Needham
    Linear Algebra and its Applications 645 (2022), 237–255 (journal link)
    MR: 4404571; Zbl: 1492.42037; doi: 10.1016/j.laa.2022.03.023; arXiv: 2108.02275 [math.FA]

  10. “Exact evaluation of the mean square radius of gyration for Gaussian topological polymer chains”
    Joint with Jason Cantarella, Tetsuo Deguchi, and Erica Uehara
    Yasuyuki Tezuka and Tetsuo Deguchi, editors, Topological Polymer Chemistry: Concepts and Practices, Springer, Singapore, 2022, 37–63 (chapter link)
    doi: 10.1007/978–981–16–6807–4_4

  11. “Expected distances on manifolds of partially oriented flags”
    Joint with Brenden Balch and Chris Peterson
    Proceedings of the American Mathematical Society 149 (2021), no. 8, 3553–3567 (journal link)
    MR: 4273156; Zbl: 1467.53060; doi: 10.1090/proc/15521; arXiv: 2001.07854 [math.DG]

  12. “Symplectic geometry and connectivity of spaces of frames”
    Joint with Tom Needham
    Advances in Computational Mathematics 47 (2021), no. 1, 5 (journal link)
    MR: 4202219; Zbl: 1464.42028; doi: 10.1007/s10444–020–09842–7; arXiv: 1804.05899 [math.FA]

  13. “Distributions of distances and volumes of balls in homogeneous lens spaces”
    Joint with Brenden Balch and Chris Peterson
    Differential Geometry and its Applications 74 (2021), 101712 (journal link)
    MR: 4192043; Zbl: 1482.53066; doi: 10.1016/j.difgeo.2020.101712; arXiv: 2004.13196 [math.DG]

  14. “New computations of the superbridge index”
    Journal of Knot Theory and Its Ramifications 29 (2020), no. 14, 2050096 (journal link)
    stick-knot-gen has supporting code and data, including bounds on superbridge index for knots through 10 crossings
    MR: 4216040; Zbl: 1460.57006; doi: 10.1142/S0218216520500960; arXiv: 2009.13648 [math.GT]

  15. “Knots with exactly 10 sticks”
    Joint with Ryan Blair, Thomas D. Eddy, and Nathaniel Morrison
    Journal of Knot Theory and Its Ramifications 29 (2020), no. 3, 2050011 (journal link)
    MR: 4101605; Zbl: 1439.57005; doi: 10.1142/S021821652050011X; arXiv: 1909.06947 [math.GT]

  16. “A fractal dimension for measures via persistent homology”
    Joint with Henry Adams, Manuchehr Aminian, Elin Farnell, Michael Kirby, Joshua Mirth, Rachel Neville, and Chris Peterson
    Nils A. Baas, Gunnar E. Carlsson, Gereon Quick, Markus Szymik, and Marius Thaule, editors, Topological Data Analysis: The Abel Symposium 2018, volume 15 of Abel Symposia, Springer, Cham, 2020, 1–31 (proceedings link)
    MR: 4338667; Zbl: 1448.62211; doi: 10.1007/978–3–030–43408–3_1; arXiv: 1808.01079 [math.DS]

  17. A geodesic between framed 200-gons “Stiefel manifolds and polygons”
    Proceedings of Bridges 2019: Mathematics, Art, Music, Architecture, Education, Culture, 187–194 (proceedings link)
    arXiv: 1902.01486 [math.HO]

  18. “Random triangles and polygons in the plane”
    Joint with Jason Cantarella, Tom Needham, and Gavin Stewart
    The American Mathematical Monthly 126 (2019), no. 2, 113–134 (journal link)
    MR: 3910627; Zbl: 1410.52004; doi: 10.1080/00029890.2019.1535735; arXiv: 1702.01027 [math.MG]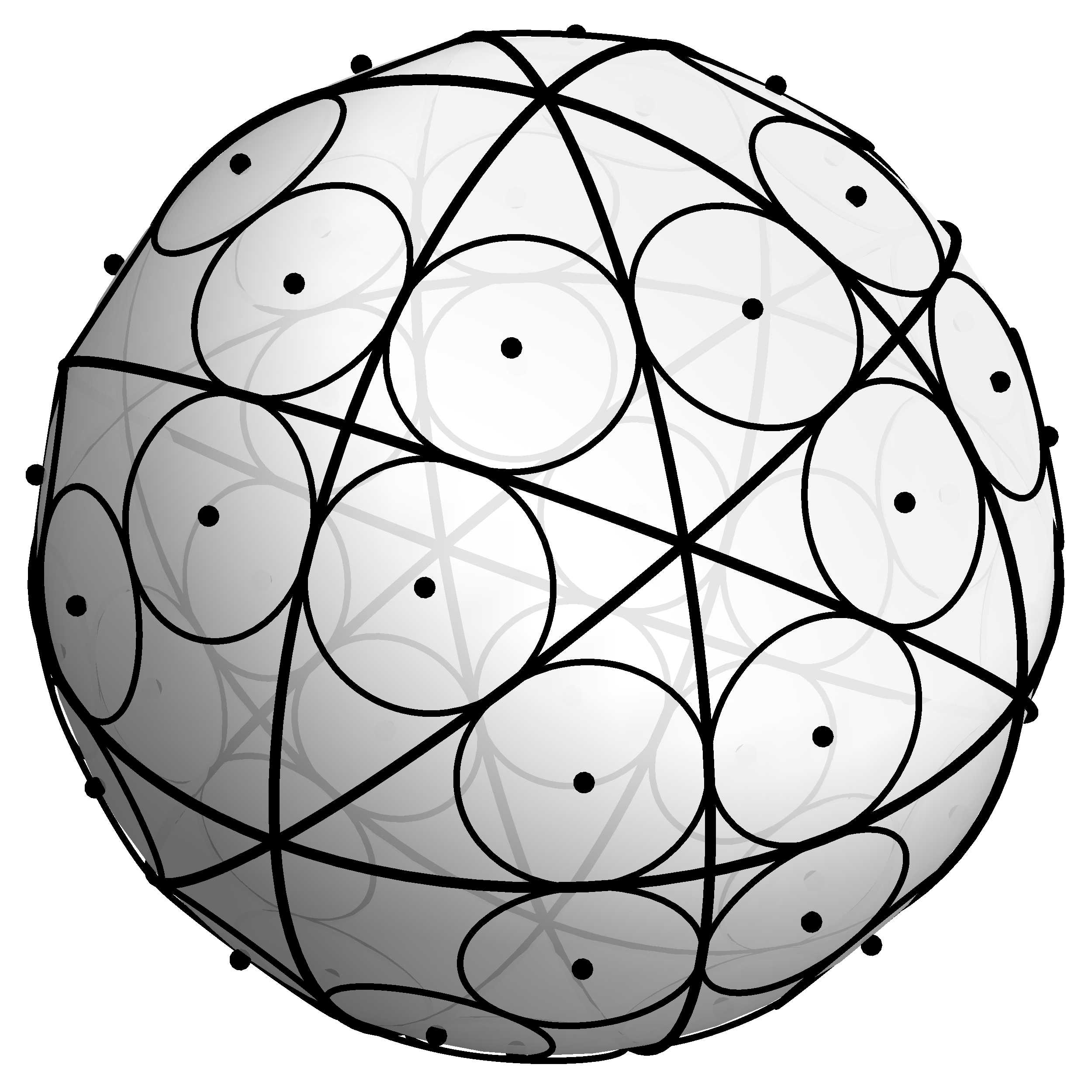

  19. Spherical tiling “Spherical geometry and the least symmetric triangle”
    Joint with Laney Bowden, Andrea Haynes, and Aaron Shukert
    Geometriae Dedicata 198 (2019), 19–34 (journal link)
    MR: 3933448; Zbl: 1418.53003; doi: 10.1007/s10711–018–0327–4; arXiv: 1708.01559 [math.MG]

  20. “The Paulsen problem made symplectic”
    Joint with Martin Ehler, Milena Hering, Christopher Manon, and Tom Needham
    Oberwolfach Reports 15 (2018), no. 4, 2790–2794 (proceedings link)
    doi (for full proceedings): 10.14760/OWR–2018–46

  21. “Symplectic geometry and frame theory”
    Joint with Tom Needham
    Oberwolfach Reports 15 (2018), no. 4, 2786–2789 (proceedings link)
    doi (for full proceedings): 10.14760/OWR–2018–46

  22. “Open and closed random walks with fixed edgelengths in ℝd”
    Joint with Jason Cantarella, Kyle Chapman, and Philipp Reiter
    Journal of Physics A: Mathematical and Theoretical 51 (2018), no. 43, 434002 (journal link)
    Special issue in honor of Stuart Whittington’s 75th birthday
    MR: 3871192; Zbl: 1409.60069; doi: 10.1088/1751–8121/aade0a; arXiv: 1806.00079 [cond-mat.stat-mech]

  23. “The geometry of constrained random walks and an application to frame theory”
    2018 IEEE Statistical Signal Processing Workshop (SSP), 343–347 (proceedings link)
    doi: 10.1109/SSP.2018.8450816

  24. “Homotopy string links and the \(\kappa\)-invariant”
    Joint with Frederick R. Cohen, Rafał Komendarczyk, and Robin Koytcheff
    Bulletin of the London Mathematical Society 49 (2017), no. 2, 246–260 (journal link)
    MR: 3656294; Zbl: 1381.55008; doi: 10.1112/blms.12025; arXiv: 1504.03233 [math.GT]

  25. “A fast direct sampling algorithm for equilateral closed polygons”
    Joint with Jason Cantarella, Bertrand Duplantier and Erica Uehara
    Journal of Physics A: Mathematical and Theoretical 49 (2016), no. 27, 275202 (journal link)
    Selected as a 2016 Highlight of J. Phys. A
    MR: 3512103; Zbl: 1342.82063 doi: 10.1088/1751–8113/49/27/275202; arXiv: 1510.02466 [cond-mat.stat-mech]

  26. “The symplectic geometry of closed equilateral random walks in 3-space”
    Joint with Jason Cantarella
    Annals of Applied Probability 26 (2016), no. 1, 549–596 (journal link)
    MR: 3449326; Zbl: 1408.53109 doi: 10.1214/15-AAP1100; arXiv: 1310.5924 [math.DG]; INI Preprint #NI13054-TOD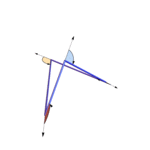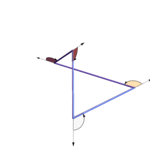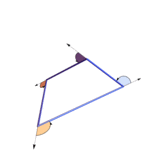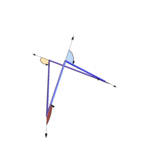

  27. Total Curvature “The expected total curvature of random polygons”
    Joint with Jason Cantarella, Alexander Y. Grosberg, and Robert Kusner
    American Journal of Mathematics 137 (2015), no. 2, 411–438 (journal link)
    MR: 3337799; Zbl: 1357.60017; doi: 10.1353/ajm.2015.0015; arXiv: 1210.6537 [math.DG]; INI Preprint #NI12084-TOD

  28. “Homotopy Brunnian links and the \(\kappa\)-invariant”
    Joint with Frederick R. Cohen and Rafał Komendarczyk
    Proceedings of the American Mathematical Society 143 (2015), no. 3, 1347–1362 (journal link)
    MR: 3293747; Zbl: 1311.57009; doi: 10.1090/S0002–9939–2014–12331–8; arXiv: 1208.4587 [math.GT]; KITP Preprint #NSF-ITP–12–163

  29. A geodesic in polygon space “Probability theory of random polygons from the quaternionic viewpoint”
    Joint with Jason Cantarella and Tetsuo Deguchi
    Communications on Pure and Applied Mathematics 67 (2014), no. 10, 1658–1699 (journal link)
    MR: 3251909; Zbl: 1300.60026; doi: 10.1002/cpa.21480; arXiv: 1206.3161 [math.DG]

  30. “The symplectic geometry of polygon space”
    Joint with Jason Cantarella
    Oberwolfach Reports 10 (2013), no. 2, 1347–1350 (proceedings link)
    doi (for full proceedings): 10.14760/OWR–2013–22

  31. A visualization of the generalized Gauss map “Generalized Gauss maps and integrals for three-component links II”
    Joint with Dennis DeTurck, Herman Gluck, Rafał Komendarczyk, Paul Melvin, Haggai Nuchi, and David Shea Vela-Vick
    Algebraic & Geometric Topology, 13 (2013), no. 5, 2897–2923 (journal link)
    MR: 3116307; Zbl: 1348.57007; doi: 10.2140/agt.2013.13.2897; arXiv: 1207.1793 [math.GT]

  32. “Poincaré duality angles and the Dirichlet-to-Neumann operator”
    Inverse Problems 29 (2013), no. 4, 045007 (journal link)
    MR: 3042083; Zbl: 1280.58003; doi: 10.1088/0266–5611/29/4/045007

  33. The Borromean rings “Generalized Gauss maps and integrals for three-component links”
    Joint with Dennis DeTurck, Herman Gluck, Rafał Komendarczyk, Paul Melvin, and David Shea Vela-Vick
    Journal of Mathematical Physics 54 (2013), no. 1, 013515 (journal link)
    MR: 3059903; Zbl: 1328.57007; doi: 10.1063/1.4774172; arXiv: 1101.3374 [math.GT]

  34. “The complete Dirichlet-to-Neumann map for differential forms”
    Joint with Vladimir Sharafutdinov
    Journal of Geometric Analysis 23 (2013), no. 4, 2063–2080 (journal link)
    MR: 3107691; Zbl: 1283.58003; doi: 10.1007/s12220–012–9320–6; arXiv: 1011.1194 [math.DG]

  35. A Legendrian knot “Legendrian contact homology and nondestabilizability”
    Joint with David Shea Vela-Vick
    Journal of Symplectic Geometry 9 (2011), no. 1, 33–44 (journal link)
    MR: 2787360; Zbl: 1226.57013; doi: 10.4310/JSG.2011.v9.n1.a3; arXiv: 0910.3914 [math.GT]

  36. Finding a higher-dimensional linking integral “Higher-dimensional linking integrals”
    Joint with David Shea Vela-Vick
    Proceedings of the American Mathematical Society 139 (2011), no. 4, 1511–1519 (journal link)
    MR: 2748445; Zbl: 1221.57038; doi: 10.1090/S0002–9939–2010–10603–2; arXiv: 0801.4022 [math.GT]

  37. The fundamental solution of the Laplacian on the two-dimensional torus “Triple linking numbers, ambiguous Hopf invariants and integral formulas for three-component links”
    Joint with Dennis DeTurck, Herman Gluck, Rafał Komendarczyk, Paul Melvin, and David Shea Vela-Vick
    Matemática Contemporânea 34 (2008), 251–283 (journal link)
    Special volume in honor of Manfredo do Carmo’s 80th birthday
    MR: 2588614; Zbl: 1194.57007; doi: 10.21711/231766362008/rmc3411; arXiv: 0901.1612 [math.GT]

  38. Absolute and relative cohomologies “Poincaré duality angles for Riemannian manifolds with boundary”
    Ph.D. thesis, University of Pennsylvania, 2009
    MR: 2713306; arXiv: 0909.1967 [math.DG]

Book Reviews

  1. Visual Differential Geometry and Forms: A Mathematical Drama in Five Acts
    Reviewed by Clayton Shonkwiler
    The American Mathematical Monthly 129 (2022), no. 8, 795–800 (journal link)
    MR: 4486025; Zbl: 1495.00007; doi: 10.1080/00029890.2022.2094677

Submitted Papers

  1. “Gaussian random embeddings of multigraphs”
    Joint with Jason Cantarella, Tetsuo Deguchi, and Erica Uehara
    arXiv: 2001.11709 [cond-mat.stat-mech]

  2. “Performance of the Uniform Closure Method for open knotting as a Bayes-type classifier”
    Joint with Emily Tibor, Elizabeth M. Annoni, Erin Brine-Doyle, Nicole Kumerow, Madeline Shogren, Jason Cantarella, and Eric J. Rawdon
    arXiv: 2011.08984 [math.GT]

  3. “Random graph embeddings with general edge potentials”
    Joint with Jason Cantarella, Tetsuo Deguchi, and Erica Uehara
    arXiv: 2205.09049 [cond-mat.stat-mech]

  4. “A faster direct sampling algorithm for equilateral closed polygons”
    Joint with Jason Cantarella and Henrik Schumacher
    arXiv: 2309.10163 [cond-mat.stat-mech]

  5. “On the existence of Parseval frames for vector bundles”
    Joint with Samuel A. Ballas and Tom Needham
    arXiv: 2312.13488 [math.DG]

Presentations

Invited Talks

Refereed Talks

Refereed Posters

Local Talks

  • Frames, Geometric Invariant Theory, and Optimization — Fragment Seminar, Colorado State University, Oct. 13, 2022.

  • What is a Random Knot? And Why Do We Care? — Math 192 Guest Lecture, Colorado State University, Sept. 23, 2021.

  • What is (Applied) Symplectic Geometry? — Who Is/What Is? Seminar, Colorado State University, Sept. 29, 2020.

  • Visualizing Higher Dimensions — CSU Math Circles, June 17 & 18, 2019.

  • Symplectic Geometry and Frame Theory — Fragment Seminar, Colorado State University, Sept. 27, 2018.

  • What’s the probability that a random triangle is obtuse? or: What the heck is a random triangle, anyway? — Math 192 Guest Lecture, Colorado State University, Sept. 27, 2016.

  • The Symplectic Geometry of Polygon Space and How to Use It — Fragment Seminar, Colorado State University, Nov. 12, 2015.

  • A New Algorithm for Sampling Closed Equilateral Random Walks — Applied Math Seminar, Colorado State University, Nov. 13, 2014.

  • Grassmannians and Random Polygons — Pattern Analysis Lab Lecture Series, Colorado State University, Nov. 6, 2014.

  • 15 Views of the Hypersphere — Math 192 Guest Lecture, Colorado State University, Oct. 10, 2014.

  • The Dirichlet-to-Neumann Operator for Differential Forms — Inverse Problems Seminar, Colorado State University, Sept. 11, 2014.

  • Closed Random Walks and Symplectic Geometry — Geometry Seminar, University of Georgia, Nov. 8, 2013.

  • Ambidextrous Knots Via Octonions — Geometry Seminar, University of Georgia, Sept. 6, 2013.

  • The Total Curvature of Random Polygons — Geometry Seminar, University of Georgia, Mar. 22, 2013.

  • Homotopy and Link Homotopy — Topology Seminar, University of Georgia, Aug. 20, 2012.

  • Generalized Gauss Maps and Triple Linking Integrals — Geometry Seminar, University of Georgia, Feb. 10, 2012.

  • Grassmannians and Random Polygons — Geometry Seminar, University of Georgia, Nov. 11, 2011.

  • The Complete Dirichlet-To-Neumann Map for Differential Forms — Geometry Seminar, University of Georgia, Sept. 2, 2011.

  • Poincaré Duality Angles for Riemannian Manifolds With Boundary — Geometry Seminar, University of Georgia, Aug. 26, 2011.

  • Poincaré Duality Angles for Riemannian Manifolds With Boundary — Ph.D. thesis defense, University of Pennsylvania, Apr. 13, 2009.

  • Recovering Cup Products from Boundary Data — Geometry–Topology Reading Seminar, University of Pennsylvania, Feb. 24, 2009.

  • Invariant Differential Forms in a Cohomogeneity One Manifold — Graduate Student Bridge Seminar, University of Pennsylvania, Feb. 18, 2009.

  • Poincaré Duality Angles for Riemannian Manifolds With Boundary — Graduate Student Geometry–Topology Seminar, University of Pennsylvania, Feb. 18, 2009.

  • The Dirichlet-To-Neumann Map for Differential Forms — Graduate Student Geometry–Topology Seminar, University of Pennsylvania, Oct. 1, 2008.

  • The Triple Linking Number Is an Ambiguous Hopf Invariant — Geometry–Topology Reading Seminar, University of Pennsylvania, Apr. 15, 2008.

  • What is a Poincaré Duality Angle? — Graduate Student Geometry–Topology Seminar, University of Pennsylvania, Apr. 2, 2008.

  • The Classification of Links up to Link-Homotopy (4 parts) — Philadelphia Area Contact/Topology Seminar, Bryn Mawr College, Nov. 8–Dec. 13, 2007.

  • Link Complements and the Classification of Links up to Link-Homotopy — Graduate Student Geometry–Topology Seminar, University of Pennsylvania, Oct. 31, 2007.

  • Geometric Linking Integrals in \(S^n \times \mathbb{R}^m\) — Pizza Seminar, University of Pennsylvania, Oct. 12, 2007.

  • Introduction to Minimal Surfaces — Pre-Colloquium Talk, University of Pennsylvania, Oct. 18, 2006.

  • The Four Vertex Theorem and its Converse — Pizza Seminar, University of Pennsylvania, Oct. 6, 2006.

  • The Gauss Linking Integral in \(S^3\) and \(H^3\) — Graduate Student Geometry–Topology Seminar, University of Pennsylvania, Sept. 27, 2006.

  • Four Isoperimetric Properties of Homogeneous Spherical Membranes — Graduate Student Geometry–Topology Seminar, University of Pennsylvania, Dec. 7, 2005.

  • Pictures and Syzygies: An Exploration of Pictures, Cellular Models and Free Resolutions — Senior Talk, The University of the South, Apr. 2003.

  • Picture Groups for Links — REU final presentation, Louisiana State University, Aug. 2002.

Notes

Some old research notes that will probably never be published.