What’s the probability that a random triangle is obtuse?
or:
What the heck is a random triangle, anyway?

Collaborators


Jason Cantarella
U. of Georgia
Thomas Needham
Ohio State
Gavin Stewart
NYU

Lewis Carroll's Pillow Problem #58
Carroll’s Answer
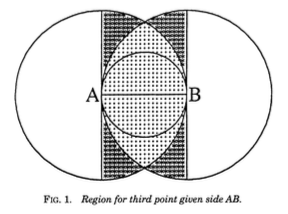
Suppose \(AB\) is the longest side. Then
\(\mathbb{P}(\text{obtuse})=\frac{\pi/8}{\pi/3-\sqrt{3}/4} \approx 0.64\)
But if \(AB\) is the second longest side,
\(\mathbb{P}(\text{obtuse}) = \frac{\pi/2}{\pi/3+\sqrt{3}/2} \approx 0.82\)
A Probabilist’s Answer
Proposition [Portnoy]: If the distribution of \((x_1,y_1,x_2,y_2,x_3,y_3)\in\mathbb{R}^6\) is spherically symmetric (for example, a standard Gaussian), then
\(\mathbb{P}(\text{obtuse}) = \frac{3}{4}\)
Consider the vertices \((x_1,y_1),(x_2,y_2),(x_3,y_3)\) as determining a single point in \(\mathbb{R}^6\).
For example, when the vertices of the triangle are chosen from independent, identically-distributed Gaussians on \(\mathbb{R}^2\).
Choose three vertices uniformly in the disk:
\(\mathbb{P}(\text{obtuse})=\frac{9}{8}-\frac{4}{\pi^2}\approx 0.7197\)
Restricted Domain?

Choose three vertices uniformly in the square:
\(\mathbb{P}(\text{obtuse})=\frac{97}{150}-\frac{\pi}{40}\approx 0.7252\)
Random Triangles?
Is Carroll’s question really about choosing random points, or is it actually about choosing random triangles?
How would you choose a triangle “at random”?
Angles?!
Remember from Geometry that three angles \((\theta_1,\theta_2,\theta_3)\) determine a triangle up to similarity (AAA).

\(\theta_1\)
\(\theta_2\)
\(\theta_3\)
What are the restrictions on the \(\theta_i\)?
\(\theta_1+\theta_2+\theta_3=\pi\)
\(0<\theta_1, 0 < \theta_2, 0<\theta_3\)
and
The Triangle of Triangles
\(\theta_1+\theta_2+\theta_3=\pi\)
\(0<\theta_1, 0 < \theta_2, 0<\theta_3\)
and
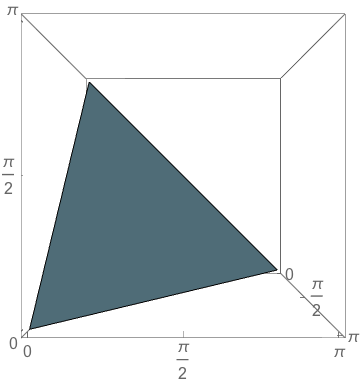
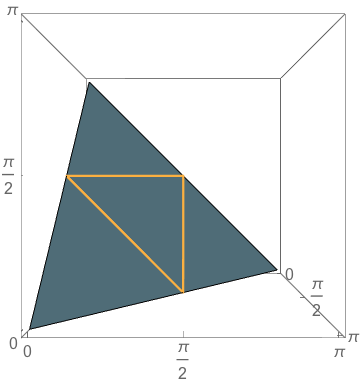
\(\theta_1=\pi/2\)
\(\theta_2=\pi/2\)
\(\theta_3=\pi/2\)
\(\mathbb{P}(\text{obtuse})=\frac{3}{4}\)
Side Lengths?!
Remember the sidelengths \((a,b,c)\) uniquely determine a triangle (SSS).
Obtuseness is scale-invariant, so pick a perimeter \(P\) and we have \(a+b+c=P\).
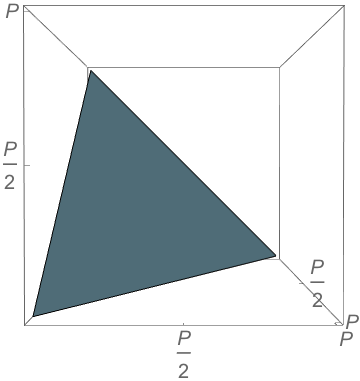
Problem
Not all points in the simplex correspond to triangles
\(b+c<a\)
\(a+b<c\)
\(a+c<b\)
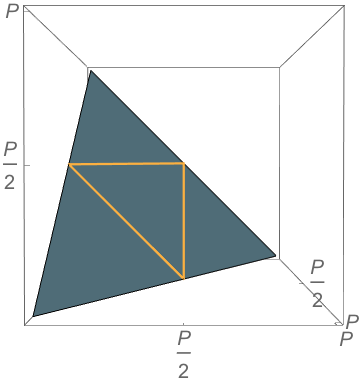
Yet Another Pillow Problem Answer
\(\mathbb{P}(\text{obtuse})=9-12\ln 2 \approx 0.68\)
\(b^2+c^2=a^2\)
\(a^2+b^2=c^2\)
\(a^2+c^2=b^2\)
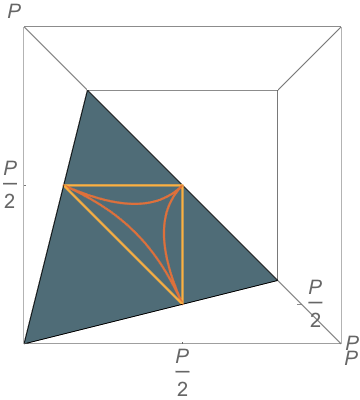

— Stephen Portnoy, Statistical Science 9 (1994), 279–284
Random Triangles...?
Translation for Geometers
The space of all triangles should be a (preferably compact) manifold \(T\) with a transitive isometry group. We should use the left-invariant metric on \(T\), scaled so vol\((T)=1\). Then the Riemannian volume form induced by this metric is a natural probability measure on \(T\), and we should compute the volume of the subset of obtuse triangles.
Ideally, this should generalize to \(n\)-gons.
Spoiler: \(T\simeq\mathbb{RP}^2=G_2\mathbb{R}^3\)
Back to Triangles
Let \(s=\frac{1}{2}(a+b+c)\) and define

Note: It’s convenient to choose \(s=1\).
\(s_a=s-a, \quad s_b = s-b, \quad s_c = s-c\)
Then
\(s_a+s_b+s_c=3s-(a+b+c)=3s-2s=s\)
and the triangle inequalities become
\(s_a>0, \quad s_b > 0, \quad s_c > 0\)
But there’s still no transitive group action!
Take Square Roots!
Consider \((x,y,z)\) so that
\(x^2=s_a, \quad y^2 = s_b, \quad z^2 = s_c\)
The unit sphere is a \(2^3\)-fold cover of triangle space

The Transitive Group
The rotations are natural transformations of the sphere, and the corresponding action on triangles is natural.
\(c=1-z^2\) fixed
\(z\) fixed
\(C(\theta) = (\frac{z^2+1}{2}\cos 2\theta, -z \sin 2\theta)\)
The equal-area-in-equal-time parametrization of the ellipse
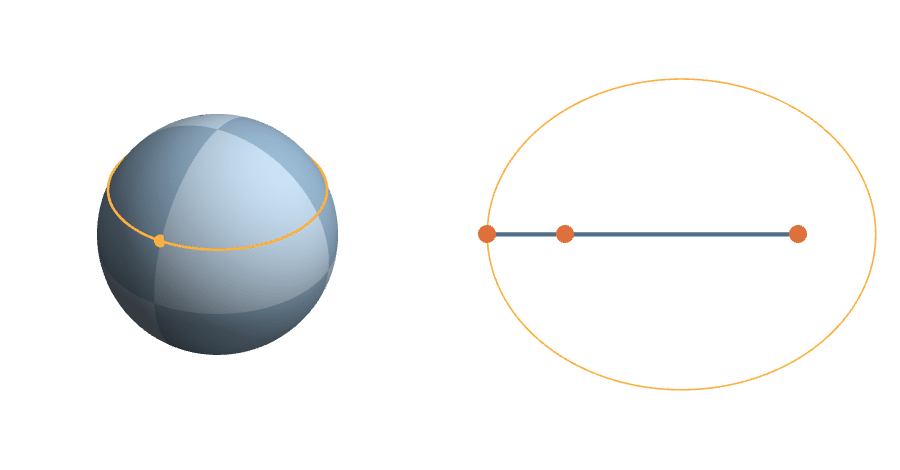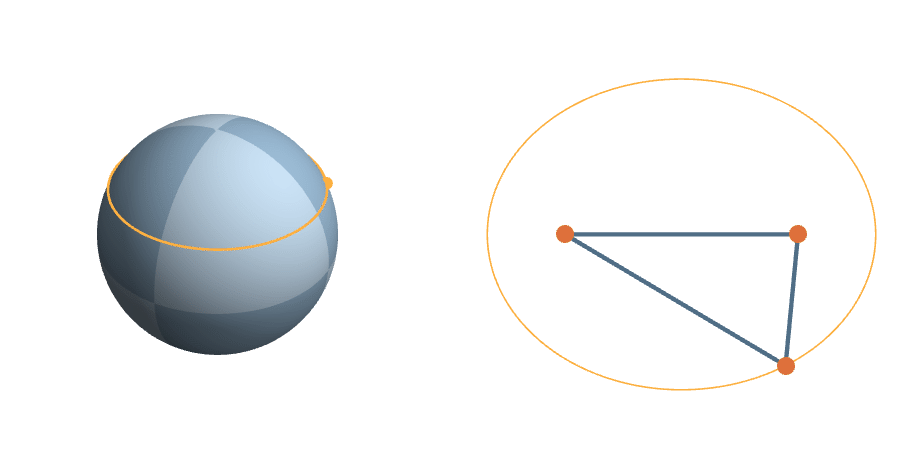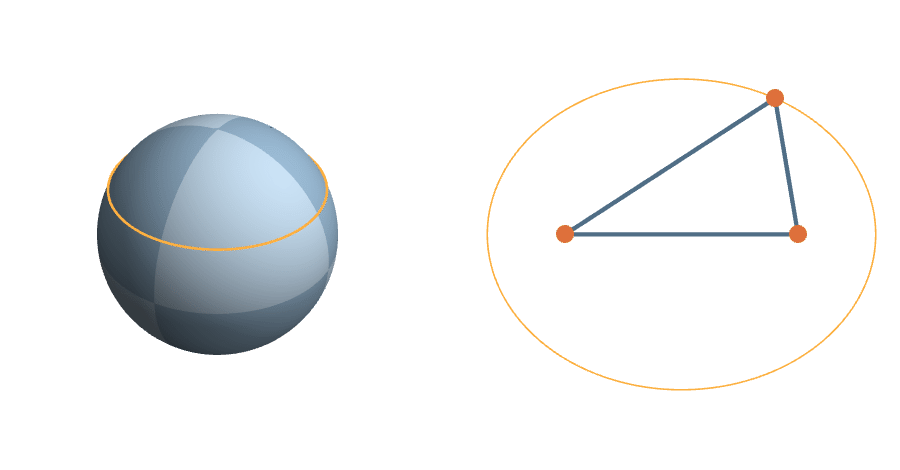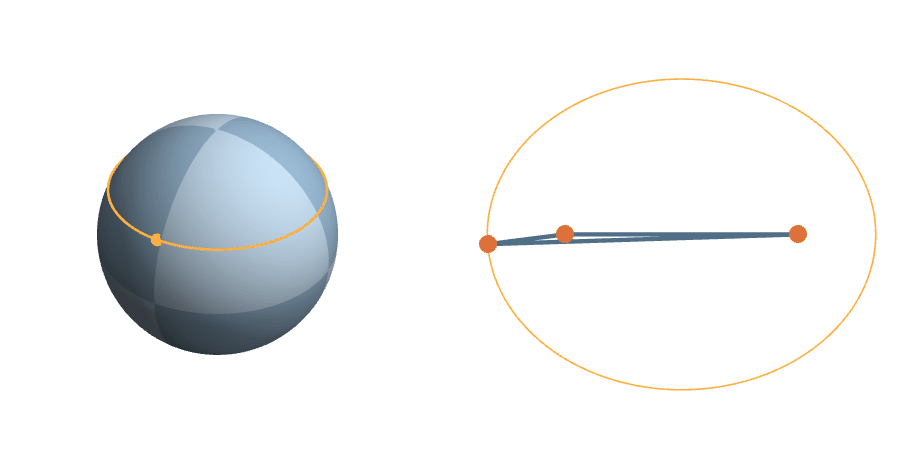
A More Complicated Rotation
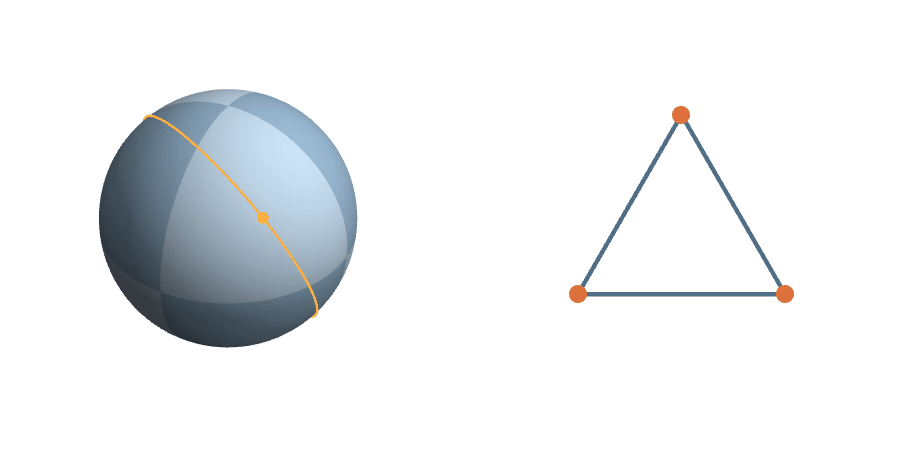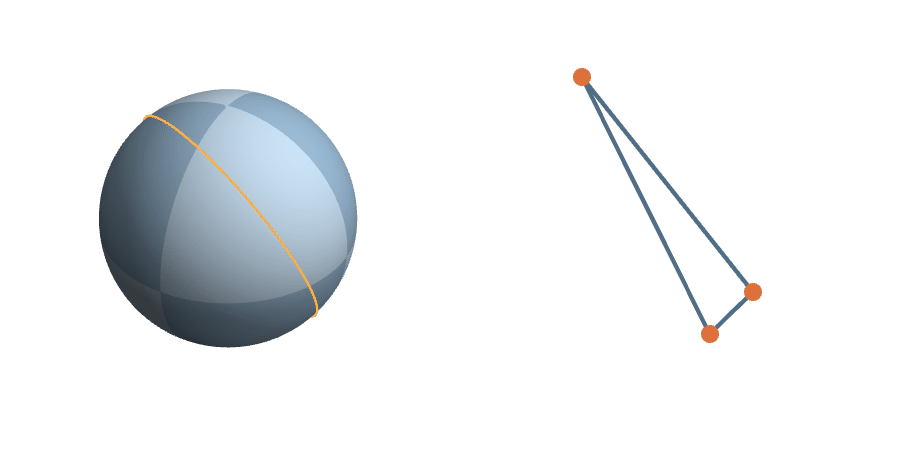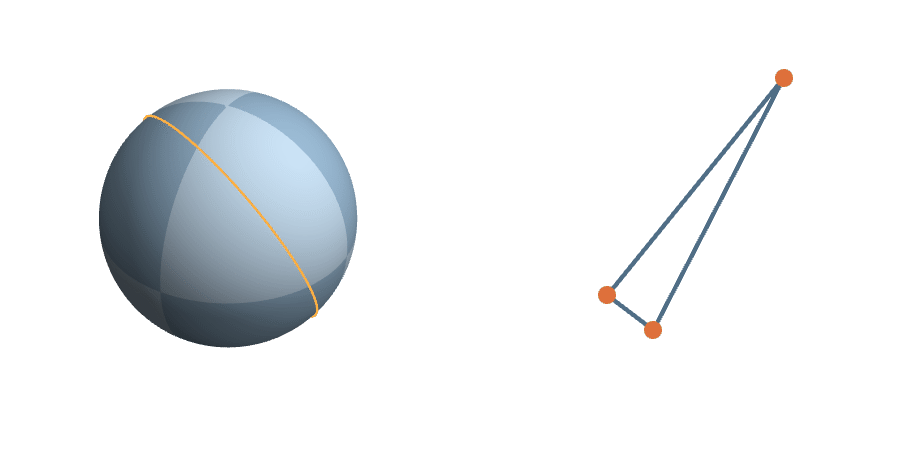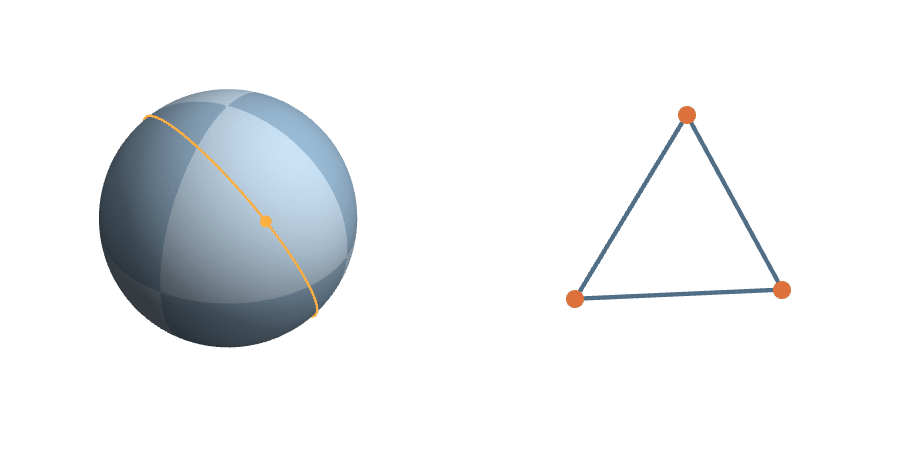
A Measure on Triangle Space
Since the uniform measure is the unique (up to scale) measure on \(S^2\) invariant under the action of \(SO(3)\)...
Definition
The symmetric measure on triangle space is the probability measure proportional to the uniform measure on the sphere.
Right Triangles
The right triangles are exactly those satisfying
\(a^2+b^2=c^2\) & permutations
Since \(a=1-s_a=1-x^2\), etc., the right triangles are determined by the quartic
\((1-x^2)^2+(1-y^2)^2=(1-z^2)^2\) & permutations
\(x^2 + x^2y^2 + y^2 = 1\), etc.

Obtuse Triangles
\(\mathbb{P}(\text{obtuse})=\frac{1}{4\pi}\text{Area} = \frac{24}{4\pi} \int_R d\theta dz\)


But now \(C\) has the parametrization
And the integral reduces to
Solution to the Pillow Problem
By Stokes’ Theorem

\(\frac{6}{\pi} \int_R d\theta dz=\frac{6}{\pi}\int_{\partial R}z d\theta = \frac{6}{\pi}\left(\int_{z=0} zd\theta + \int_C zd\theta \right)\)
\(\left(\sqrt{\frac{1-y^2}{1+y^2}},y,y\sqrt{\frac{1-y^2}{1+y^2}}\right)\)
\(\frac{6}{\pi} \int_0^1 \left(\frac{2y}{1+y^4}-\frac{y}{1+y^2}\right)dy\)
Our Answer
Theorem [w/ Cantarella, Needham, Stewart]
With respect to the symmetric measure on triangles, the probability that a random triangle is obtuse is
\(\frac{3}{2}-\frac{3\ln 2}{\pi}\approx0.838\)
Generalization
For \(n>3\), the sidelengths do not uniquely determine an \(n\)-gon, so the simplex approach doesn‘t obviously generalize.
Key Observation: The coordinates \((x,y,z)\) of a point on the sphere are the Plücker coordinates of the perpendicular 2-plane.
\(\vec{p}=\vec{a} \times \vec{b}\)
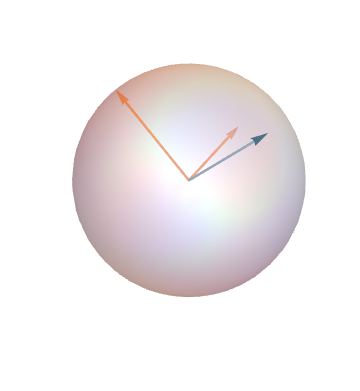
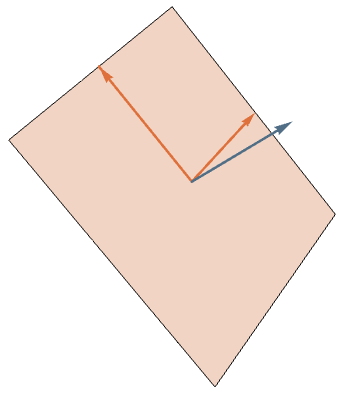
Planes and Polygons
In general, we can identify the collection of planar \(n\)-gons with \(G_2(\mathbb{R}^n)\), the Grassmannian of 2-planes through the origin in \(\mathbb{R}^n\).
Definition [w/ Cantarella & Deguchi]
The symmetric measure on \(n\)-gons of perimeter 2 up to translation and rotation is the pushforward of Haar measure on \(G_2(\mathbb{R}^n)\).
Sylvester’s Four Point Problem
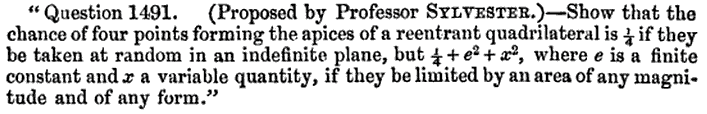

convex
reflex/reentrant
self-intersecting
Modern Reformulation: What is the probability that all vertices of a random quadrilateral lie on its convex hull?
Some Answers
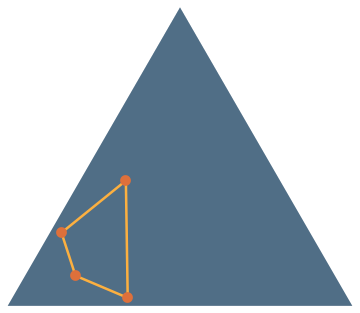
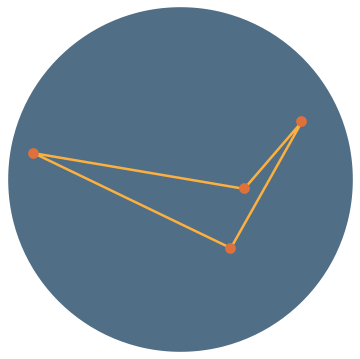
\(\mathbb{P}(\text{reflex})=\frac{1}{3}\)
\(\mathbb{P}(\text{reflex})=\frac{35}{12\pi^2}\approx 0.296\)
Theorem [Blaschke]

\(\frac{35}{12\pi^2}\leq\mathbb{P}(\text{reflex})\leq\frac{1}{3}\)
Our Answer
Theorem [w/ Cantarella, Needham, Stewart]
With respect to the symmetric measure, each of the three classes of quadrilaterals occurs with equal probability. In particular, \(\mathbb{P}(\text{reflex})=\frac{1}{3}\).
More generally...
Theorem [w/ Cantarella, Needham, Stewart]
With respect to any permutation-invariant measure on \(n\)-gon space, the probability that a random \(n\)-gon is convex is \(\frac{2}{(n-1)!}\).
Polygons in Space
There is a version of this story for polygons in \(\mathbb{R}^3\) as well.
Example Theorem [w/ Cantarella, Grosberg, Kusner]
The expected total curvature of a random space \(n\)-gon is exactly
\(\frac{\pi}{2}n + \frac{\pi}{4} \frac{2n}{2n-3}\)
The polygon space is \(G_2(\mathbb{C}^n)\) and the analog of the squaring map is the Hopf map.

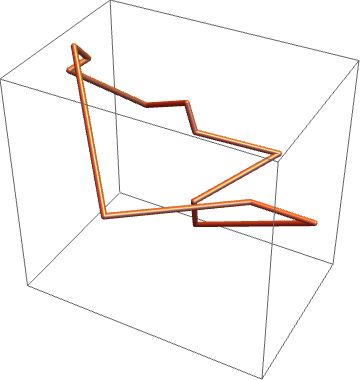
Open Problem
What is the manifold of equilateral planar \(n\)-gons up to translation and rotation?
Is there a good parametrization of this manifold?
Thank you!
References
- J. Cantarella, T. Deguchi, and C. Shonkwiler. Probability theory of random polygons from the quaternionic perspective. Communications on Pure and Applied Mathematics 67 (2014), 1658–1699.
- J. Cantarella, A. Y. Grosberg, R. Kusner, and C. Shonkwiler. Expected total curvature of random polygons. American Journal of Mathematics 137 (2015), 411–438.
- J. Cantarella, T. Needham, C. Shonkwiler, and G. Stewart. Random triangles and polygons in the plane. Coming soon!
Square Roots of Angles
It turns out that if we take square roots of angles instead, we get:
\(\mathbb{P}(\text{obtuse}) = \frac{4-2\sqrt{2}}{\sqrt{\pi}} \approx 0.661\)
But this approach doesn’t seem to generalize nearly as well as taking square roots of edgelengths.
