Software and Code

Symmetric Molecule-Based Feature Detector (SymFD, previously CoShREM)
Topological Data Analysis to Support Image Analysis Tasks in Environmental Science
Musisep
Testing isomorphism between tuples of subspaces
Topological data analysis of cloud images
Symmetry of low complexity, uniquely optimal codes
Neural network Sobolev training
Gaussian mean width and ReLU singular values
Gabor-Steiner Equiangular Tight Frames
BinderFinder
Equiangular Lines by Pillar Decomposition
Haar Wavelet-Based Perceptual Similarity Index (HaarPSI)
ShearLab [from FG Angewandte Funktionalanalysis at TU Berlin]  

Symmetric Molecule-Based Feature Detector (SymFD, previously CoShREM)

SymFD is a MATLAB toolbox providing methods for the detection and analysis of edges, ridges, and blobs in 2D images by utilizing the special symmetry properties of directionally sensitive 2D analyzing functions. Its predecessor, the Complex Shearlet-Based Edge and Ridge Measure (CoShREM) Toolbox, can also be downloaded here.

The image of a monarch butterfly used in the examples below is part of the LIVE Image Quality Assessment Database. The shown results can be reproduced by calling the respective scripts in the 'Examples' folder in the SymFD toolbox.

Edge Detection:

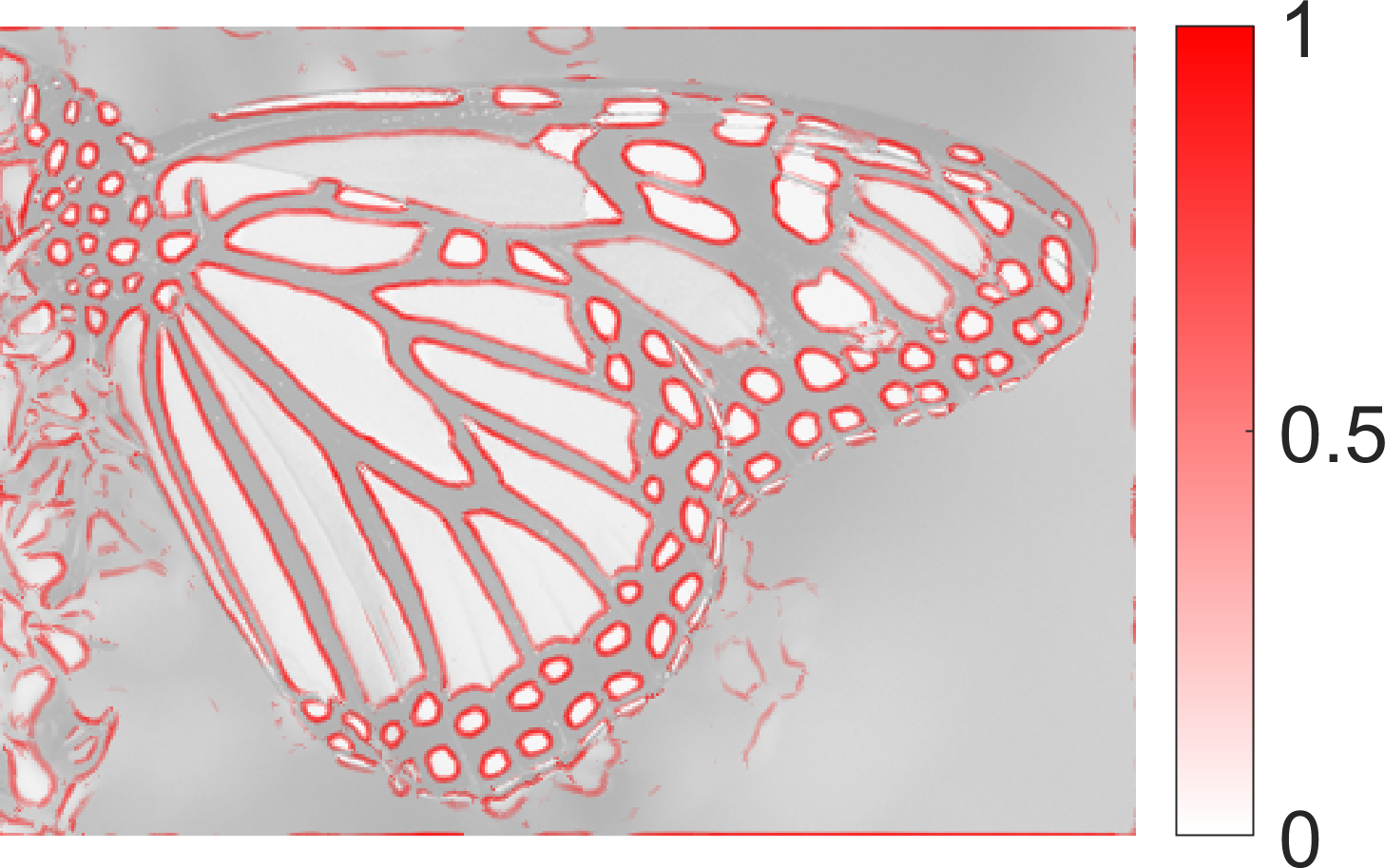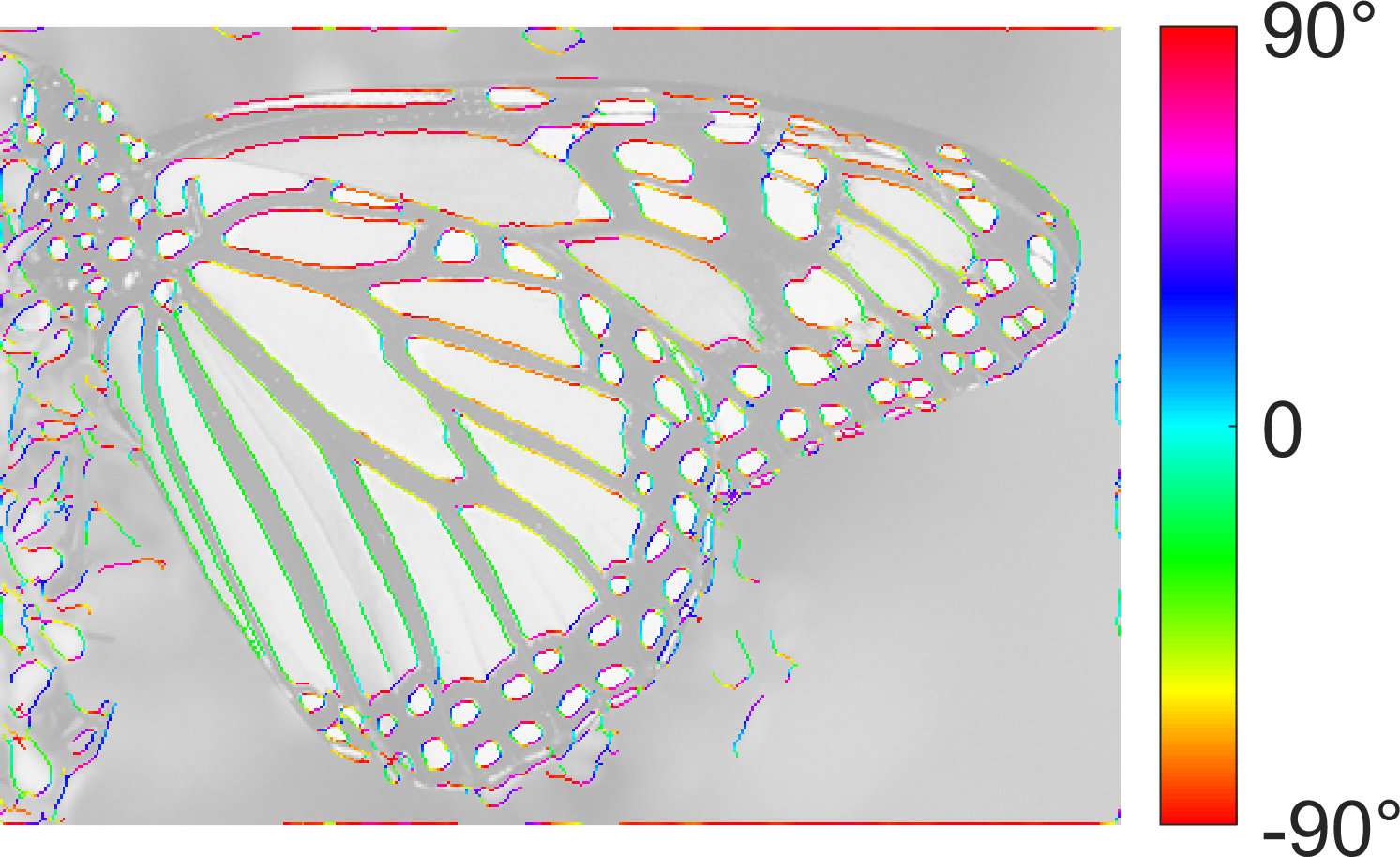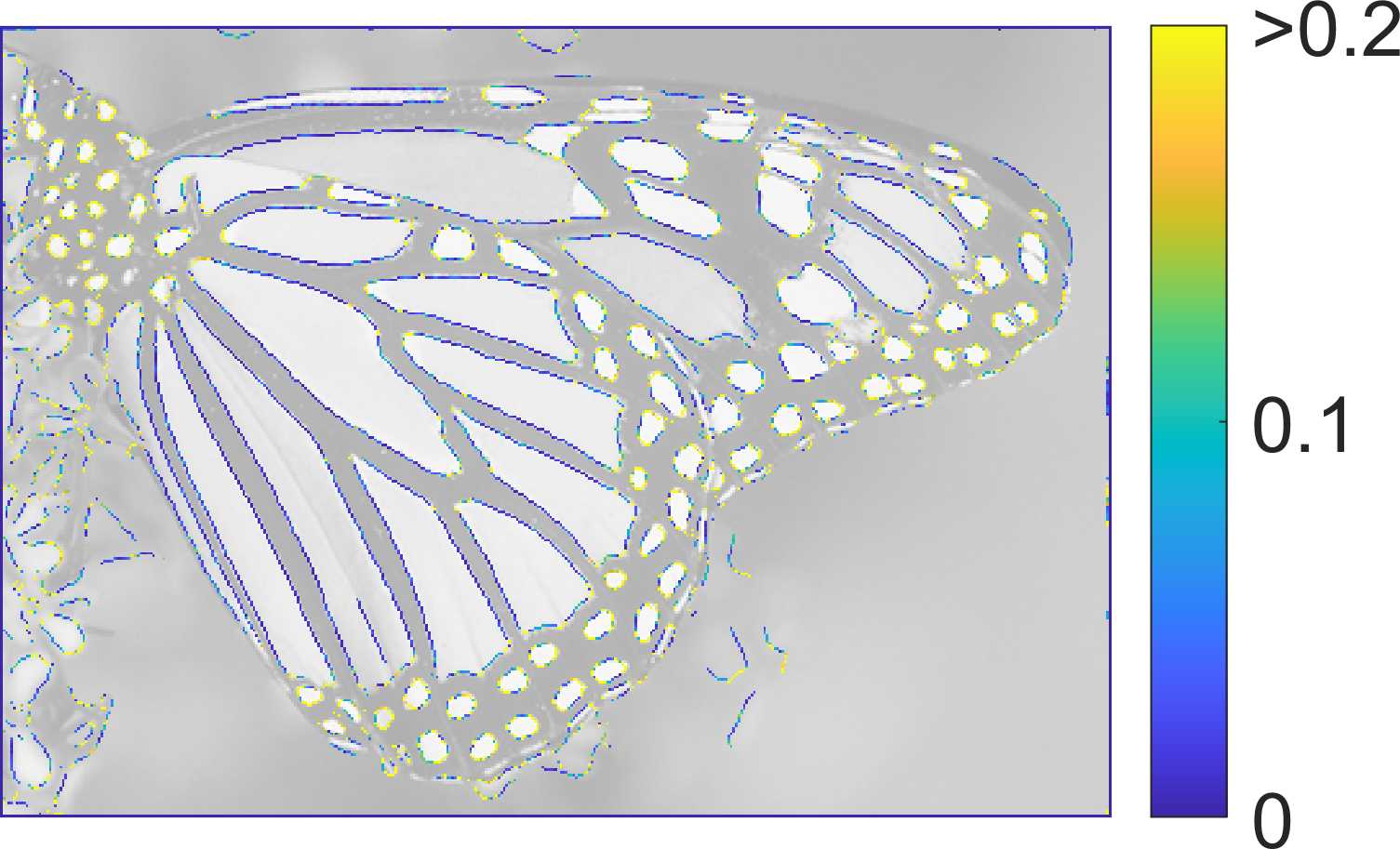SymFD Edge Measure	Tangent Directions	Curvature

Ridge Detection:

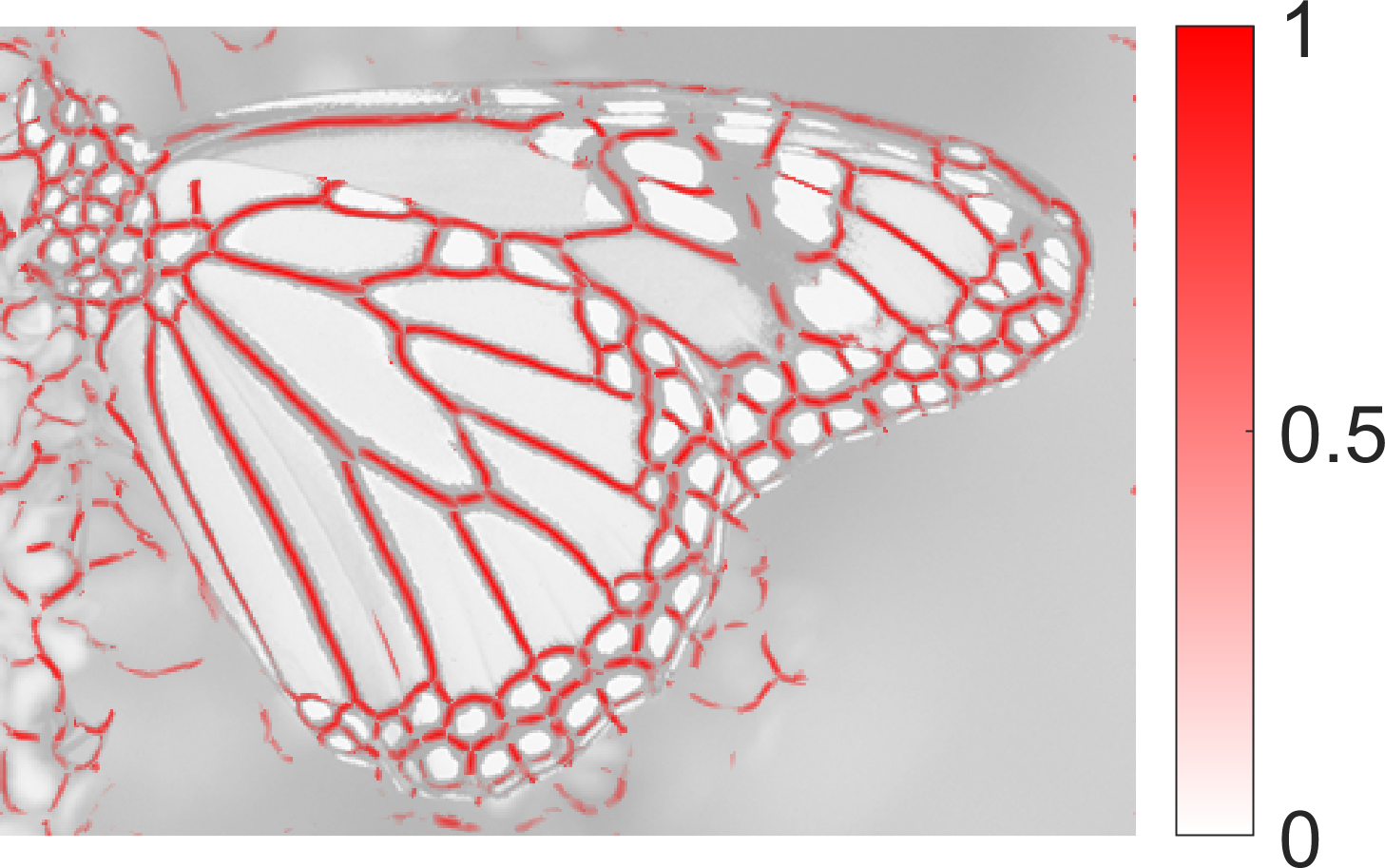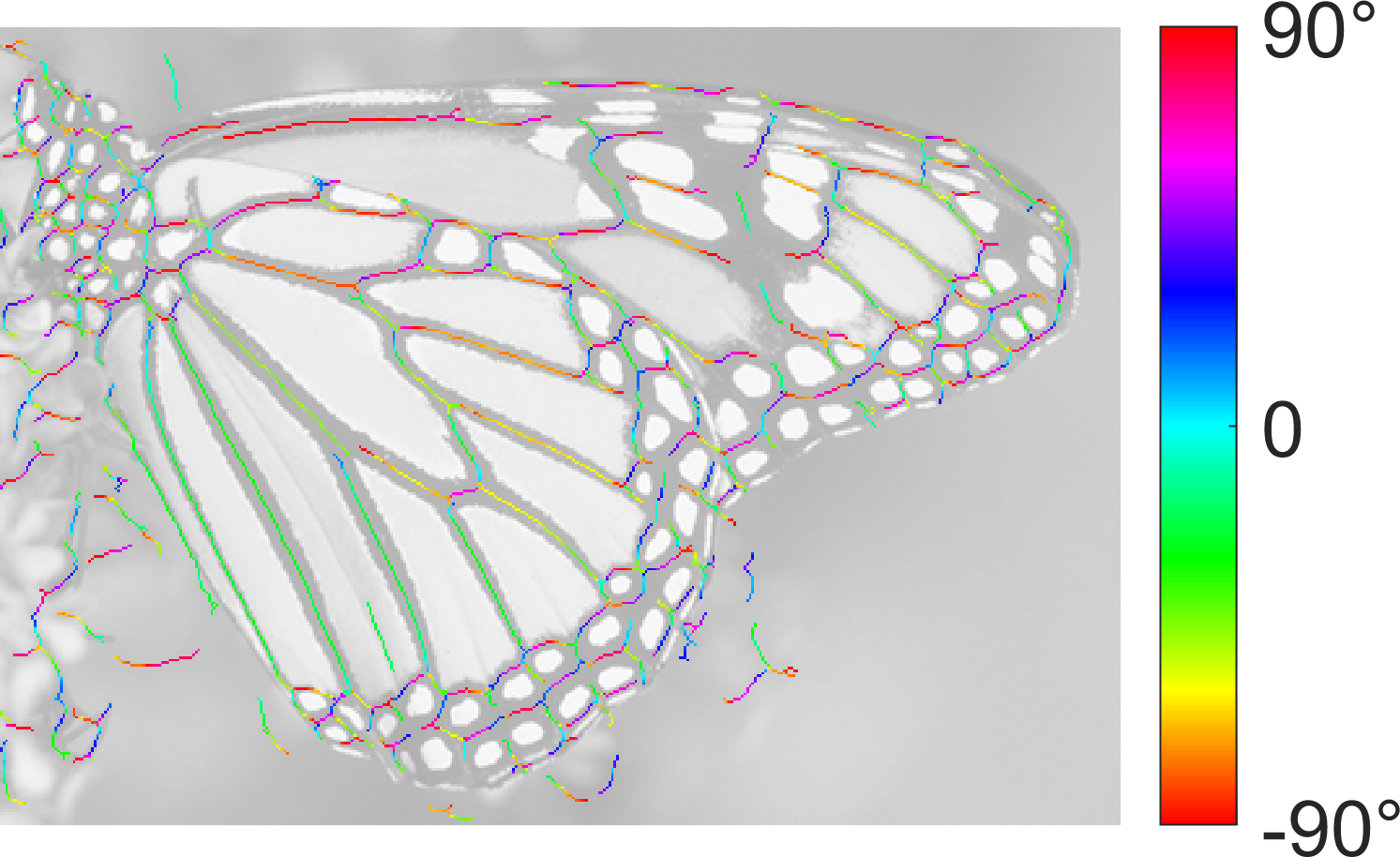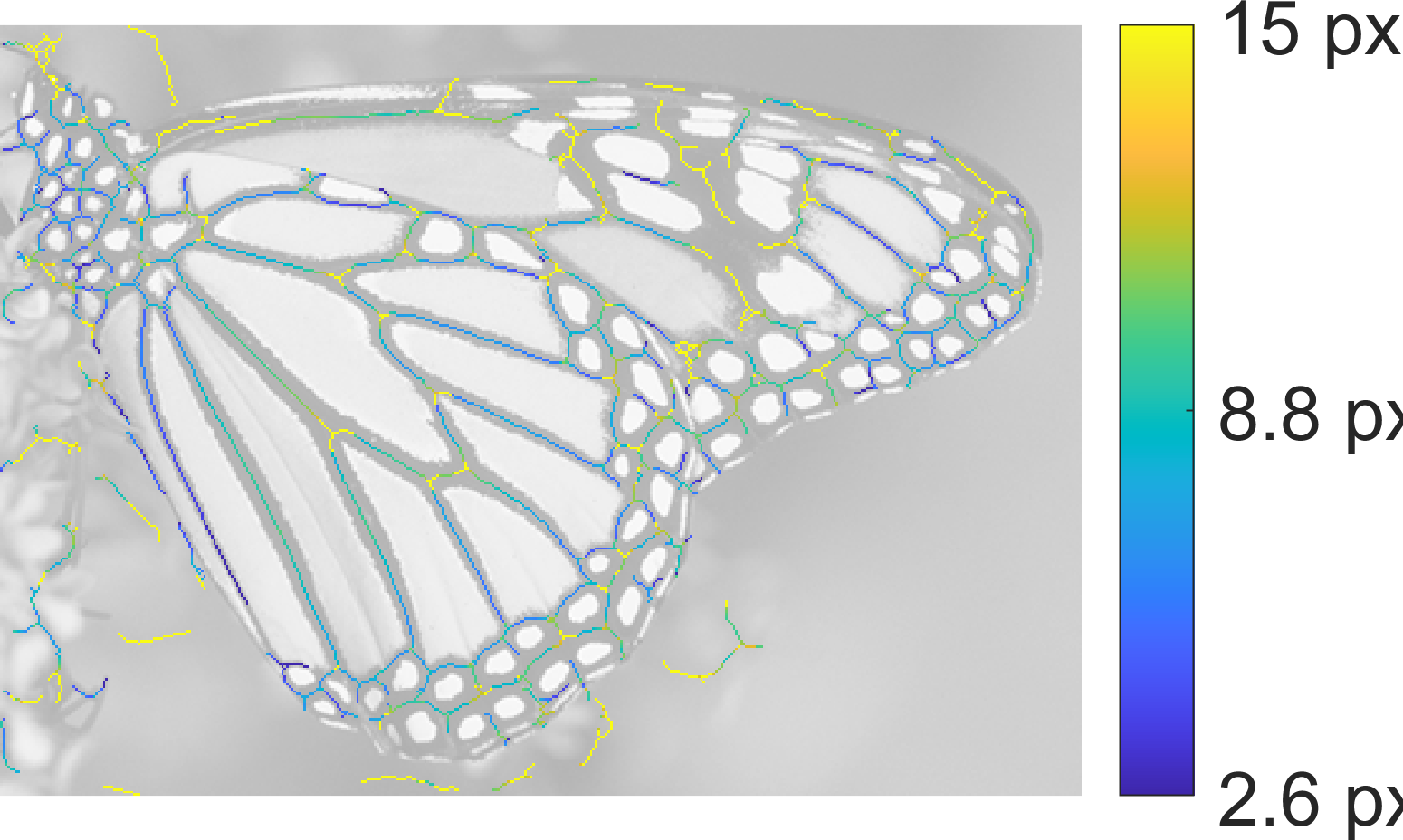SymFD Ridge Measure	Tangent Directions	Ridge Widths

Blob Detection:

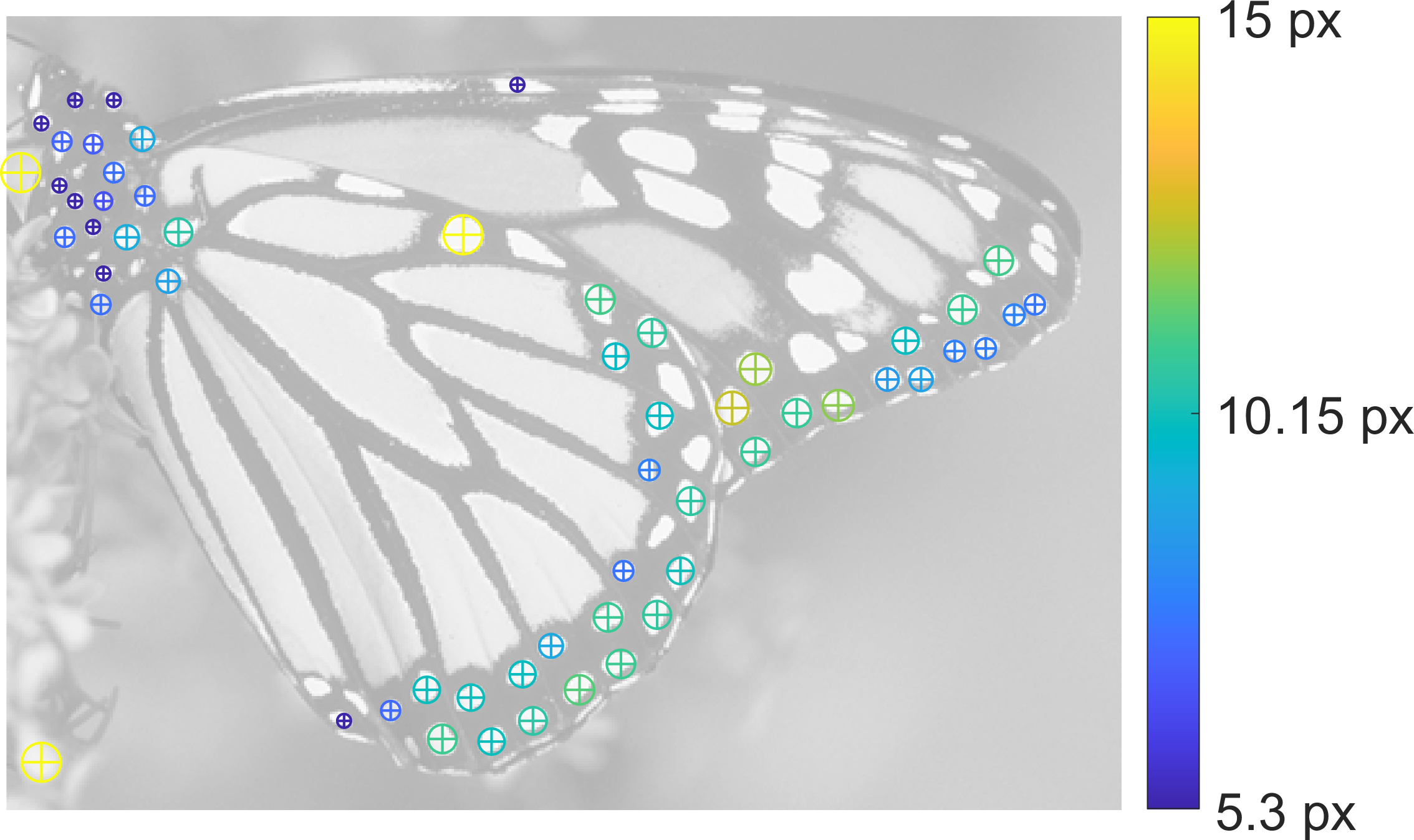Detected Blobs

Downloads:

• SymFD Toolbox 1.1 for MATLAB (.zip)
• SymFD Toolbox Parameter Guide (.pdf)
• SymFD Numerical Experiments (.zip)
• The SymFD Toolbox for MATLAB can be found on Github and on MathWorks File Exchange
• CoShREM Toolbox 1.1 for MATLAB (.zip)
• The CoShREM Toolbox for Python can be found on GitHub and on PyPI.
  The package can directly be installed form the command line by calling: sudo pip3 install pycoshrem.
• CoShREM Toolbox Parameter Guide (.pdf)
• MATLAB scripts and all detection results from "Shearlet-Based Detection of Flame Fronts" (.zip)
• Video of detected flame fronts (.avi)

Publications:

1. R. Reisenhofer, E. J. King
   Edge, Ridge, and Blob Detection with Symmetric Molecules (PDF). Supplementary Materials (PDF).
   To appear: SIAM Journal on Imaging Sciences, 2019.
2. R. Reisenhofer, J. Kiefer and E. J. King
   Shearlet-Based Detection of Flame Fronts (PDF)
   Experiments in Fluids, vol. 57(3), 41:1-41:14, 2016.
   doi:10.1007/s00348-016-2128-6
3. E. J. King, R. Reisenhofer, J. Kiefer, W.-Q Lim, Z. Li and G. Heygster
   Shearlet-Based Edge Detection: Flame Fronts and Tidal Flats (PDF)
   Applications of Digital Image Processing XXXVIII (Andrew G. Tescher, ed.), SPIE Conference Series, vol. 9599, 2015. doi:10.1117/12.218865
4. R. Reisenhofer
   The Complex Shearlet Transform and Applications to Image Quality Assessment (PDF)
   Technische Universität Berlin, Master's Thesis, 2014.

Topological Data Analysis to Support Image Analysis Tasks in Environmental Science

A Github repository of code used in “A Primer on Topological Data Analysis to Support Image Analysis Tasks in Environmental Science” by Lander Ver Hoef, Henry Adams, Emily J. King, Imme Ebert-Uphof (Artificial Intelligence for the Earth Systems, vol. 2, no. 1) is here.

Musisep

A Python program to blindly separate the contributions of different instruments in an audio recording via dictionary learning.

Two variants are available:

1. An algorithm which uses a pitch-invariant time-frequency representation that enables it to identify patterns of peaks in the spectrum corresponding to sounds of musical instruments via a sparse pursuit algorithm. Further refinement via non-linear optimization makes it independent of the tuning of the instruments and incorporates inharmonicity.
   Sören Schulze, Emily J. King: Sparse Pursuit and Dictionary Learning for Blind Source Separation in Polyphonic Music Recordings. EURASIP J. Audio Speech Music Process. 2021. doi:10.1186/s13636-020-00190-4.
2. An algorithm based on the same model but using a deep neural network with policy gradients to directly interpret the complex-valued STFT output.
   Sören Schulze, Johannes Leuschner, Emily J. King: Blind Source Separation in Polyphonic Music Recordings Using Deep Neural Networks Trained via Policy Gradients. 2021. arXiv:2107.04235

These are the separation results of the first algorithm for the 8th piece from the 12 Basset Horn Duos by Wolfgang A. Mozart (KV 487) in an arrangement by Alberto Gomez Gomez (license: CC BY-NC-SA 3.0) for two recorders, played on acoustic soprano recorder and violin:

• Mixed audio:
  
• Algorithmically separated recorder track:
  
• Algorithmically separated violin track:
  

The code is on GitHub. Test data (ZIP) and the API documentation are also available.

Testing isomorphism between tuples of subspaces

Given two tuples of subspaces, or more precisely, orthonormal bases for those subspaces, can you tell whether the tuples are isomorphic? Some algorithms to test for isomorphism are posted here.
Code to compute an injective invariant (normalized Gram) for tuples in the Grassmannian of planes in \(\mathbb{R}^d\) modulo \(O(d)\) given a Gram matrix of orthobases for those planes is here.
Code to compute words which may be evaluated on a generated \(H^\ast\)-algebra to determine an injective invariant is here.
Code to compute traces of the evaluated words to determine isomorphism of \(n\)-tuples of \(d \times \) matrices generating \(H^\ast\)-algebra here.

For more information, see Algoritm 1, Algorithm 2, and Lemma 11 in "Testing isomorphism between tuples of subspaces" by Emily J. King, Dustin G. Mixon, and Shayne Waldron.

Topological data analysis of cloud images

In collaboration with Lander Ver Hoef, Yoonjin Lee, Henry Adams, and Imme Ebert-Uphoff, topological data analysis tools are being developed to analyze cloud data, in particular to automatically identify convection in GOES-R imagery. To be notified when the software is released, sign up here.

Symmetry of low complexity, uniquely optimal codes

Solutions to geometric extremal problems often exhibit a notably high degree of symmetry. In a recent paper, it is shown that the concept of "optimality implies (partial) symmetry" holds in a number of settings. Some of the proofs are computer-assisted; the code has been uploaded as ancillary files in the arXiv version of the paper.

For more information, see "Uniquely optimal codes of low complexity are symmetric" by Christopher Cox, Emily J. King, Dustin G. Mixon, and Hans Parshall.

Neural network Sobolev training

After fixing an architecture and an exactly \(m\)-times differentiable activation function \(\rho\), the set of realized neural networks is not closed in the order-\((m-1)\) Sobolev space \(W^{m-1,p}\). We further show that this set is not closed in \(W^{m,p}\) under slightly stronger conditions on the \(m\)-th derivative of \(\rho\). For a real analytic activation function, we show that the set of realized neural networks is not closed in \(W^{k,p}\) for any \(k \in \mathbb{N}\). These results suggest that training a network to approximate a target function in Sobolev norm does not prevent parameter explosion.

However, using this code, we show that a particular network is still capable of closely approximating a non-network target function with network parameters that grow at a manageable rate relative to the approximation error.

For more information, see Nonclosedness of the Set of Neural Networks in Sobolev Space by Scott Mahan, Emily King, and Alex Cloninger.

Gaussian mean width and ReLU singular values

ReLU singular values are a generalization of singular values to maps generated by the composition of an affine linear map and a component-wise application of the rectified linear unit.  For Python code to approximate ReLU singular values, click here. Gaussian mean width is a measure — in some sense — of dimensionality of data.  It can be used to differentiate between data that is correctly or incorrectly classified in a trained discriminative neural network.  For Python code to calculate the Gaussian mean width of finite data, click here.

For more information, see "Singular Values for ReLU Layers" by Soren Dittmer, Emily J. King, and Peter Maass.

Gabor-Steiner Equiangular Tight Frames

A Gabor-Steiner equiangular tight frame is generated as the orbit of a special fiducial vector under a reducible projective representation of the Weyl-Heisenburg group. As equiangular tight frames, Gabor-Steiner equiangular tight frames satisfy a Parseval-like equality and span lines which have constant pairwise angle.  Further, Gabor-Steiner equiangular tight frames have large numbers of embedded simplices. (See BinderFinder below.)

A short Matlab code to generate Gabor-Steiner equiangular tight frames via Weyl-Heisenburg groups over \(\mathbb{Z}_m\) and \(\mathbb{Z}_m \times \mathbb{Z}_n\) for odd \(m, n \geq 3\) may be downloaded here.

For more information, see "Optimal arrangements of classical and quantum states with limited purity" by Bernhard Bodmann and Emily J. King, (PDF), to appear Journal of the London Mathematical Society, 2019.

BinderFinder

A regular simplex is a collection of s+1 equiangular vectors which form a tight frame for their span, which is s-dimensional. The binder of an equiangular tight frame (ETF) consists of all of the subsets of the index set which correspond to regular simplices. Such simplices, if they exist, must have the same size as the spark of the frame and thus are also the smallest circuits in the matroid associated to the frame. Directly computing the binder is very computationally expensive. A few different mathematical tricks are employed in the code of BinderFinder in order to make computing the binder of some larger ETFs tractable. The code is a short Matlab program (which is also Octave compatible).

Download the code here: BinderFinder.m

For more information, see "Equiangular tight frames that contain regular simplices" by Matthew Fickus, John Jasper, Emily J. King, and Dustin G. Mixon. (PDF)

Equiangular Lines by Pillar Decomposition

By combining the pillar decomposition of Lemmens and Seidel 1973 with the semidefinite programming approach of Bachoc and Vallentin 2008 and Barg and Yu 2014 and further arguments from combinatorics and linear algebra, one is able to prove lower upper bounds on the size of sets of equiangular lines in various dimensions which are in some cases significantly better than the previously known bounds.

For more information, see the paper "New Upper Bounds for Equiangular Lines by Pillar Decomposition" by Emily J. King and Xiaoxian Tang, PDF. The code and supplementary materials may be found here.

Haar Wavelet-Based Perceptual Similarity Index (HaarPSI)

The Haar wavelet-based perceptual similarity index (HaarPSI) is a similarity measure for images that aims to correctly assess the perceptual similarity between two images with respect to a human viewer.

In most practical situations, images and videos can neither be compressed nor transmitted without introducing distortions that will eventually be perceived by a human observer. Vice versa, most applications of image and video restoration techniques, such as inpainting or denoising, aim to enhance the quality of experience of human viewers. Correctly predicting the similarity of an image with an undistorted reference image, as subjectively experienced by a human viewer, can thus lead to significant improvements in any transmission, compression, or restoration system.

For more information and downloads please visit www.haarpsi.org. The HaarPSI is also available on github.

ShearLab [from FG Angewandte Funktionalanalysis at TU Berlin]

The inpainted images that appear in the papers [KKZ14] and [KKL13] were generated by ShearLab, developed in part by former group member Rafael Reisenhofer.