I study isomorphism in algebra, which asks how do we tell two algebras apart.
Over more than a century, researchers have puzzled over this unsolved question with various motives.
It is an exciting time in the subject with advances that have improved exponentially over what
we could do even 5 years ago.
What follows is one present day application with a substantial pay off. I hope it will
be a gentel introduction, appropriate for students and anyone curious, into some of the work I do.
The Goal: Make data coordinate free.
| Your data |
= What is really changing. |
| Our isomorphism tests |
Measurement makes observations into numbers. To do that, we
seem to need coordiantes and scales. E.g. fix xyz directions,
choosing meters or feet, assigning each color a number, etc..
In real data, repeated measurements cannot guarantee
the same coordinates. This creates a problem.
Data is senstive to coordinates.
How can we tell if data has changed, or if we just
recorded the same event but in different coordinates?
A closer look at coordinate problems.
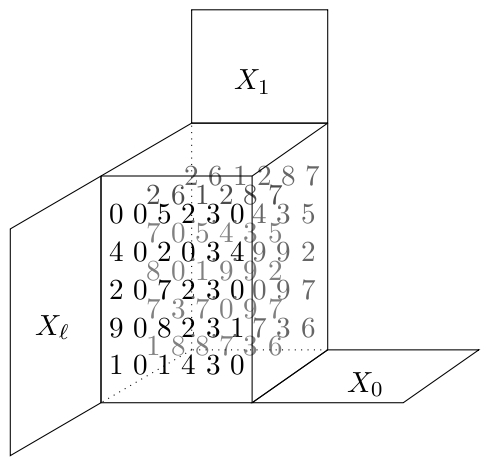
I think of data as uniform tables of numbers (you may need to fill
in missing numbers with 0).
E.g. a digital picture measures the color of point $(x,y)$ in an image,
recording it as pixel $T_{xy}$. We might also add coordinates $RGB$ to
interpet color as "Red", "Blue", "Green", which we do by adding a
3rd dimension to our frame of reference, e.g. $T_{xy}^{RGB}$.
Predictable coordinate changes include changing lengths of $x$ and $y$,
e.g. centimeters to inches. Or swapping Red-Blue-Green (RGB) with
Cyan-Yellow-Grayscale (CYK). Here official standards take care of of
organizing the converstion of coordinates. So data recorded in
on coordinate system is easy to compare with data recorded in another,
so long as we are told about the system of coordinates.
Difficult coordinate changes
result when we cannot even know what coordinates are involved.
Consider the following.
-
Every day you take a picture of a leaf to look for changes,
but you cannot reposition the camera identically each time.
Your xy-coordinates change over time. Changes in color scales
can occur if you buy a new camera and many other subtle changes.
-
You need a table of the network traffic between computers.
Each computer gets an address but that address is randomly
assigned and changes over time. Over time different collections
of the same data may shuffle the orders in the table with no
practical method to keep track.
-
Metadata is the result of processing other data, e.g. by taking
gradiants, symmetires, or other functions on our given information.
That processing necessitates often arbitrary and even randomized
choices within the algorithms that produce the metadata. Controlling
for the resulting coordinates is either too complex or at times a
theoretical impossibility.
My approach to coordinate-free data.
I convert data into algebra where the effects of coordinates have
predictable effects, known as isomorphism.
What makes algebra a natural tool for data.
Algebra is the study of equation solving. You have two problems:
- invent numbers to call the solutions, and
- make algorithms that find solutions.
For example, to solve $x+2=1$ you invent negative numbers along with
algorithms for subtraction. For $3x=2$ you invent fractions along with
the division algorithm. Perhaps most instructive is $x^2+1=0$ where the
integers have no solution, complex numbers have $2$ solutions, meanwhile
the quarternions you encounter in calculus have at least $6$ obvious
solutions: $\pm i$, $\pm j$, and $\pm k$. In fact, the quarternions
have
infinitely many solutions to the quadratic equation $x^2+1=0$.
So Different number systems give different solutions to the same
equations.
However, if we change our coordinates or write our algebras with
completely different symbols, for example as follows, the solutions
to our equations remain the same!
| $1$ |
$i$ |
$j$ |
$k$ |
| $(1,0,0,0)$ |
$(0,1,0,0)$ |
$(0,0,1,0)$ |
$(0,0,0,1)$ |
| $\begin{bmatrix} 1 & 0 \\ 0 & 1\end{bmatrix}$ |
$\begin{bmatrix} \sqrt{-1} & 0 \\ 0 & \sqrt{-1}\end{bmatrix}$ |
$\begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix}$ |
$\begin{bmatrix} 0 & \sqrt{-1} \\ -\sqrt{-1} & 0\end{bmatrix}$ |
The moral:
- Data that is different gives different algebras.
- The same data in different coordinates gives equal algebras.
- Most algebra has algorithms behind it to make these features accessible.