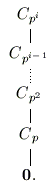
|
|
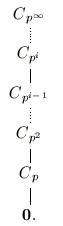
|
|
Copyright (c) 2003-2004 James B. Wilson | Show Frames | Hide Frames
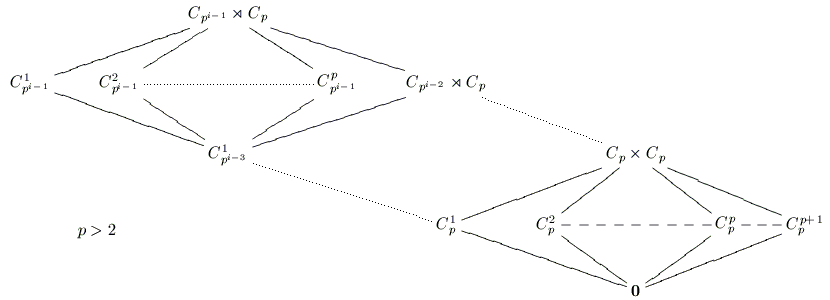
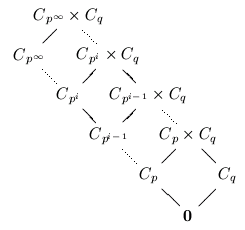
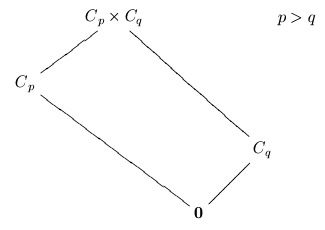
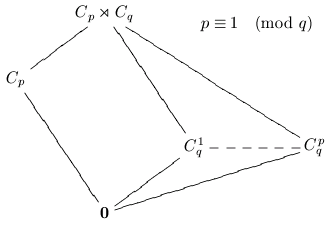
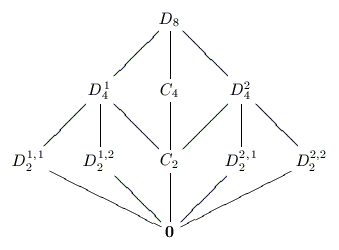
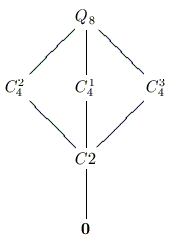
The following diagrams are the lattices of the only outerplanar groups.
A group is called outerplanar if its subgroup lattice can be drawn so that the resulting graph is outerplanar. This means all the subgroup vertices lie on the unbounded face of the graph embedded in the plane.
The Classification of Outerplanar Groups
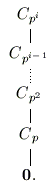
|

|
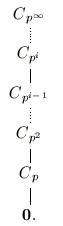
|

|
|
|
|
|
|
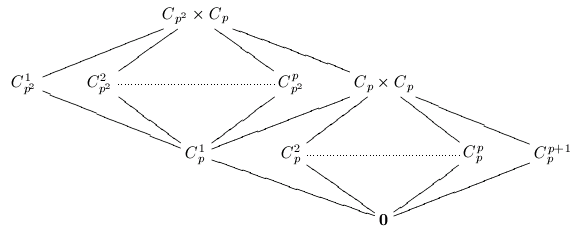
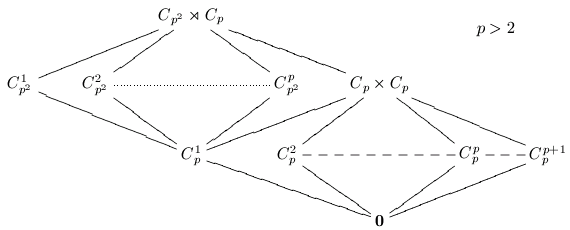
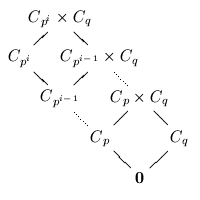
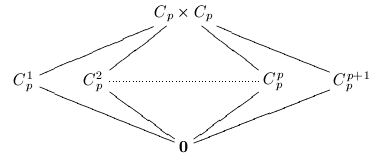
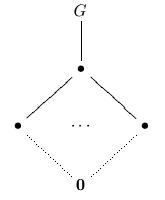
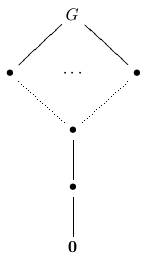
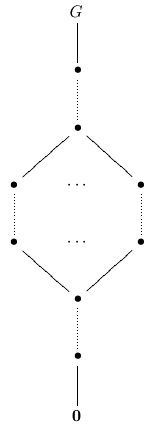
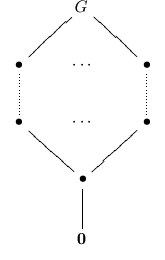
The general classification of planar groups involves a particular case of the extension problem. For example, we look at the group C_p x C_p and attempt to "glue" the diamond shapes together along the exterior edges. Along the way an important restriction is determined: with the exception of a few exceptional cases, there are no acyclic groups with a unique minimal subgroup, or with a unique maximal subgroup. This means we do not need to consider groups that "stack" a planar group atop a chain of groups, or below. That is, the following lattices are impossible for groups.
|
|
|
| i = 0, 1, 2 | i = 3 | i = 4 | i > 4 | |
| p=2 | All |
C8 C4 x C2 D8 Q8 |
C16 C8 x C2 C8 x_t C2 Q16 |
C2^i C2^{i-1} x C2 C2^{i-1} x_t C2 |
| p>2 | All |
Cp^3 Cp^2 x Cp Cp^2 x_t Cp |
Cp^4 Cp^3 x Cp Cp^3 x_t Cp |
Cp^i Cp^{i-1} x Cp Cp^{i-1} x_t Cp |