Combinatorics

BlueBox  

Enumeration and Structure

Course Notes – MATH 501/2

LaTeX-ed on August 25, 2025

Alexander Hulpke
Department of Mathematics
Colorado State University
1874 Campus Delivery
Fort Collins, CO, 80523 Title graphics:
Window in the Southern Transept of the Cathedral in Cologne (detail) Gerhard Richter These notes are accompanying my course MATH 501/2, Combinatorics, held Fall 2025 at Colorado State University.

©2025 Alexander Hulpke. Copying for personal use is permitted.

1 Preface

Counting is innate to man. History of India
Abū Rayhān Muhammad ibn Ahmad Al-Bīrūnī

This are lecture notes I prepared for a graduate Combinatorics course which ran in 2016/17, 2020/21, 2024 and 2025 at Colorado State University.

They started many years ago from an attempt to supplement the book  [cameron] (which has great taste in selecting topics, but sometimes is exceedingly terse) with further explanations and topics, without aiming for the encyclopedic completeness of [stanley1, stanley2].

In compiling these notes, In addition to the books already mentioned, I have benefitted from: [cameron, cameronlint, godsilroyle, lidlniederreiterapp, lintwilson, hall, concrete, knuth3, reichmeider].

You are welcome to use these notes freely for your own courses or students – I’d be indebted to hear if you found them useful.

Fort Collins,
Alexander Hulpke
hulpke@colostate.edu

Chapter 0 Introduction

A combinatorial structure is one which has combinatorial properties. Combinatorial properties are those possessed by combinatorial structures. So formal definitions are not getting us anywhere.
We shall leave combinatorial structure as an undefined term. […]Course on Undergraduate Combinatorics
Solomon Golomb and Andy Liu

1 What is Combinatorics?

If one looks at university mathematics classes around 1920, one already finds the basic pattern of many current courses. Single-variable analysis had already taken much of its present shape. Algebra had begun to formalize groups, rings, and fields — concepts that, a few years later, looked very much like what is taught today. Much of the theory of differential equations was known, and numerical methods lacked only the availability of fast computers. But there was little combinatorics beyond the basic counting formulas used in statistics. Combinatorics began to grow suddenly in the 1950s and 1960s, in part motivated by the advent of computers, and arguably did not have a standard list of topics until the 1980s or 1990s. It differs from many other areas of mathematics in that it was not driven by a small number of deep (often unresolved) problems, but by the observation that problems from seemingly different areas actually follow similar patterns and can be studied with similar methods. Its scope, in the broadest sense, is the study of the different ways objects can be related to one another.

This investigation naturally splits into three parts: The question of existence (Can certain configurations exist?) Counting the number of possible configurations. (If we can count them it often implies we have a good overview over what can exist.) And finding extreme, often optimal, cases.

This course looks at combinatorics split into two main areas, roughly corresponding to semesters: the first is enumerative combinatorics, the study of counting the different ways configurations can be set up. The second is the study of properties of combinatorial structures that consists of many objects subject to certain prescribed conditions.

2 Prerequisites

This being a graduate class we shall assume knowledge of some topics that have been covered in undergraduate classes. In particular we shall use:

Sets, Functions, Relations

We assume the reader is comfortable with the concept of sets and standard constructs such as Cartesian products. We denote the set of all subsets of $X$ by $𝒫(X)$, it is called the power set of $X$.

A relation on a set $X$ is a subset of $X\times X$, functions can be considered as a particular class of relations. We thus might consider a function $f:X\to Y$ as a subset of $X\times Y$.

Another important class of relations are equivalence relations. Via equivalence classes they correspond to partitions of the set.

Induction

The technique of proof by induction is intimately related to the concept of recursion. It is assumed, that the reader is comfortable with the various variants (different starting values, referring to multiple previous values, postulating a smallest counterexample) of finite induction. We also might sometimes just state that a proof follows by induction, if base case or inductive step are obvious or standard.

1 Abstract Algebra

Abstract algebra is often useful in providing a formal framework for describing objects. We assume the reader is familiar with the standard concepts from an undergraduate abstract algebra class – groups, permutations (we multiply permutations from left to right), cycle form, polynomial rings, finite fields, and linear algebra.

2 Graph Terminology

This being a graduate class, the assumption is that the reader has encountered the basic definitions of graph theory – such as: vertex, edge, degree, directed/undirected, path, tree – already in an undergraduate class.

3 Calculus

It often comes as a surprise to students , that combinatorics – this epitome of discrete mathematics – uses techniques from calculus. Some of it is the classical use of approximations to estimate growth, but we shall also need it as a toolset for manipulating power series. Still, there is no need for the reader to worry that we would encounter messy approximations, convergence tests, or bathtubs that are filled while simultaneously draining.

3 OEIS

A problem that arises often in combinatorics is that we can easily describe small examples, but that it is initially hard to see the underlying patterns. For example, we might be able to count the total number of objects of small size, but will be unable to count how many there are of larger size. In investigating such situations, the Online Encyclopedia of Integer Sequences (OEIS, at oeis.org) is an invaluable tool that allows to look up number sequences that fit the particular pattern Given by a few values , and for many of these gives a huge number of connections and references . Sequences in this encyclopedia have a “storage number” starting with the letter ”A”, and we will refer to these at times by an indicator box OEIS A002106.

Chapter 1 Basic Counting

One of the basic tasks of combinatorics is to determine the cardinality of (finite) classes of objects. Beyond basic applicability of such a number – for example to estimate probabilities – the actual process of counting may be of interest, as it gives further insight into the problem:

• If we cannot count a class of objects, we cannot claim that we know it.

• The process of enumeration might – for example by giving a bijection between classes of different sets – uncover a relation between different classes of objects.

• The process of counting might lend itself to become constructive, that is allow an actual construction of (or iteration through) all objects in the class.

The class of objects might have a clear mathematical description – e.g., all subsets of the set $\{1,\mathrm{\dots },5\}$. In other situations the description itself needs to be translated into proper mathematical language. For example:

Definition 1 (Derangements, informal definition).

Given $n$ letters and $n$ addressed envelopes, a derangement is an assignment of letters to envelopes such that no letter is in the correct envelope.

(How many derangement of $n$ exist? This particular problem will be solved in section 5.)

Here the translation to more formal objects is that we consider the letters and envelopes to be numbered from $1$ to $n$, and the assignment being a function. That is:

Definition 2 (Derangements).

For an integer $n$, a derangement is a bijection $d:N\to N$ on $N=\{1,\mathrm{\dots },n\}$ (i.e. a permutation), such that $d(i)\ne i$ for all $i\in N$.

We will start in this chapter by considering the enumeration of some basic constructs – sets and sequences. More interesting problems, such as the derangements here, arise later if further conditions restrict to sub-classes, or if obvious descriptions could have multiple sequences describe the same object.

1 Basic Counting of Sequences and Sets

I am the sea of permutation.
I live beyond interpretation.
I scramble all the names and the combinations.
I penetrate the walls of explanation. Lay My Love
Brian Eno

The number of elements of a set $A$, denoted by $\left|A\right|$ (or sometimes as $\mathrm{\#}A$) and called its cardinality, is defined as the unique $n$, such that there is a bijective function from $A$ to $\{1,2,\mathrm{\dots },n\}$.

There are three basic principles that underlie counting:

Disjoint Union

If $A=A_1\cup A_2$ with $A_1\cap A_2=\mathrm{\varnothing }$, then $\left|A\right|=\left|A_1\right|+\left|A_2\right|$.

Cartesian product

$\left|A\times B\right|=\left|A\right|\cdot \left|B\right|$.

Equivalence classes

If we can represent each element of $A$ in $m$ different ways by elements of $B$, then $\left|A\right|=\left|B\right|\cdot m$.

A sequence (or tuple) of length $k$ is simply an element of the $k$-fold cartesian product. Entries are chosen independently, that is if the first entry has $a$ choices and the second entry $b$, there are $a\cdot b$ possible choices for a length two sequence. Thus, if we consider sequences of length $k$, entries chosen from a set $A$ of cardinality $n$, there are $n^k$ such sequences.

This allows for duplication of entries, but in some cases – arranging objects in sequence – this is not desired. In this case we can still choose $n$ entries in the first position, but in the second position need to avoid the entry already chosen in the first position, giving $n-1$ options. (The number of options is always the same, the actual set of options of course depends on the choice in the first position.) The number of sequences of length $k$ thus is ${(n)}_k=n\cdot (n-1)\cdot (n-2)\cdot \mathrm{\cdots }\cdot (n-k+1)=\frac{n!}{(n-k)!}$, called “$n$ lower factorial $k$”.

This could be continued up to a sequence of length $n$ (after which all $n$ element choices have been exhausted). Such a sequence is called a permutation of $A$. There are $n!={(n)}_n=n\cdot (n-1)\cdot \mathrm{\cdots }\cdot 2\cdot 1$ such permutations.

Next we consider sets of elements. While every duplicate-free sequence describes a set, sequences that have the same elements arranged in different order describe the same set. Every set of $k$ elements from $n$ thus will be described by $k!$ different duplicate-free sequences. To enumerate sets, we therefore need to divide by this factor, and get for the number of $k$-element sets from $n$ the count given by the binomial coefficient

$$\left(\genfrac{}{}{0pt}{}{n}{k}\right)=\frac{{(n)}_k}{k!}=\frac{n!}{(n-k)!k!}$$

Note (using a convention of $0!=1$) we get that $\left(\genfrac{}{}{0pt}{}{n}{0}\right)=\left(\genfrac{}{}{0pt}{}{n}{n}\right)=1$. It also can be convenient to define $\left(\genfrac{}{}{0pt}{}{n}{k}\right)=0$ for or $k>n$.

Often one counting process can be modified to count somewhat different objects: Consider compositions of a number $n$ into $k$ parts, that is ways of writing $n$ as a sum of exactly $k$ positive integers with ordering being relevant. For example $4=2+2=1+3=3+1$ are the 3 possible compositions of $4$ into $2$ parts.

To get a formula of the number of possibilities, write the maximum composition

$$n=1+1+1+\mathrm{\cdots }+1$$

which has $n-1$ plus-signs. We obtain the possible compositions into $k$ parts by grouping summands together to only have $k$ summands. That is, we designate $k-1$ plus signs from the given $n-1$ possible ones as giving us the separation. The number of possibilities thus is $\left(\genfrac{}{}{0pt}{}{n-1}{k-1}\right)$.

If we also want to allow summands of $0$ when writing $n$ as a sum of $k$ terms, we can simply assume that we temporarily add $1$ to each summand. This guarantees that each summand is positive, but adds $k$ to the sum. We thus count the number of ways to express $n+k$ as a sum of $k$ summands which is by the previous formula $\left(\genfrac{}{}{0pt}{}{n+k-1}{k-1}\right)$.

Check this for $n=4$ and $k=2$.

Again, slightly rephrasing the problem, this is also the number of multisets, that is set-like collections in which we allow the same element to appear multiple times, with $n$ elements chosen from $k$ possibilities, the $i$-th summand indicating how often the $i$-th element is chosen.

Swapping the role of $n$ and $k$, We denote by $\left(\left(\genfrac{}{}{0pt}{}{n}{k}\right)\right)=\left(\genfrac{}{}{0pt}{}{n+k-1}{n-1}\right)=\left(\genfrac{}{}{0pt}{}{n+k-1}{k}\right)$ (the second equality follows from Prop.4 a) the number of $k$-element multisets chosen from $n$ possibilities.

The results of the previous paragraphs are summarized in the following theorem:

Theorem 3.

The number of ways to select $k$ objects from a set of $n$ is given by the following table:

	Repetition	No Repetition
Order significant	$n^k$	${(n)}_k$
(sequences)
Order not significant	$\left({\displaystyle \genfrac{}{}{0pt}{}{n+k-1}{k}}\right)=\left(\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right)\right)$	$\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right)$
(sets)

Note 1.1.

Instead of using the word significant some books talk about ordered or unordered sequences. I find this confusing, as the use of ordered is opposite that of the word sorted which has the same meaning in common language. We therefore use the language of significant.

2 Bijections and Double Counting

As long as there is no double counting, Section 3(a) adopts the principle of the recent cases allowing recovery of both a complainants actual losses and a misappropriator’s unjust benefit… Draft of Uniform Trade Secrets Act
American Bar Association

In this section we consider two further important counting principles that can be used to build on the basic constructs.

Instead of counting a set $A$ of objects directly, it might be easiest to establish a bijection to another set $B$, that is a function $f:A\to B$ which is one-to-one (also called injective) and onto (also called surjective). Once such a function has been established we know that $\left|A\right|=\left|B\right|$ and if we know $\left|B\right|$ we thus have counted $\left|A\right|$.

We used this idea already above when we were counting compositions by instead considering possible positions of plus signs.

As a further example, consider the following problem: We have an $n\times n$ grid of points with horizontal and vertical connections (depicted in figure 1 for $3\times 3$) and want to count the number of different paths from the bottom left, to the top right corner, that only go right or up.

Figure 1: A $3\times 3$ grid

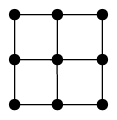
Each such path thus has exactly $n-1$ right steps, and $n-1$ up steps. We thus (this already could be considered as one bijection) could count instead $0/1$ sequences ($0$ is right, $1$ is up) of length $2n-2$ that contain exactly $n-1$ ones (and zeros). Denote the set of such sequences by $A$.

To determine $\left|A\right|$, we observe that each sequence is determined uniquely by the positions of the ones and there are exactly $n-1$ of them. Thus let $B$ be the set of all $(n-1)$-element subsets of $\{1,\mathrm{\dots },2n-2\}$.

We define $f:A\to B$ to assign to a sequence the positions of the ones, $f:a_1,\mathrm{\dots },a_{2n-2}\mapsto \{i\mid a_i=1\}$.

As every sequence has exactly $n-1$ ones, indeed $f$ goes from $A$ to $B$. As the positions of the ones define the sequence, $f$ is injective. And as we clearly can construct a sequence which has ones in exactly $n-1$ given positions, $f$ is surjective as well. Thus $f$ is a bijection.

We know that $\left|B\right|=\left(\genfrac{}{}{0pt}{}{2n-2}{n-1}\right)$, this is also the cardinality of $A$.

Check this for $n=2$, $n=3$.

The second useful technique is to “double counting”, counting the same set in two different ways (which is a bijection from a set to itself). Both counts must give the same result, which can often give rise to interesting identities. The following lemma is an example of this paradigm:

Lemma 2.1 (Handshaking Lemma).

At a convention (where not everyone greets everyone else but no pair greets twice), the number of delegates who shake hands an odd number of times is even.

Proof 2.2.

we assume without loss of generality that the delegates are $\{1,\mathrm{\dots },n\}$. Consider the set of handshakes

$$S=\{(i,j)\mid i\text{ and }j\text{ shake hands.}\}.$$

We know that if $(i,j)$ is in $S$, so is $(j,i)$. This means that $\left|S\right|$ is even, $\left|S\right|=2y$ where $y$ is the total number of handshakes occurring.

On the other hand, let $x_i$ be the number of pairs with $i$ in the first position. We thus get $\sum x_i=\left|S\right|=2y$. If a sum of numbers is even, there must be an even number of odd summands.

But $x_i$ is also the number of times that $i$ shakes hands, proving the result.

About binomial theorem I’m teeming with a lot o’ news,
With many cheerful facts about the square of the hypotenuse. The Pirates of Penzance
W.S. Gilbert

The combinatorial interpretation of binomial coefficients and double counting allows us to easily prove some identities for binomial coefficients (which typically are proven by induction in undergraduate classes):

Proposition 4.

Let $n,k$ be nonnegative integers with $k\le n$. Then:

• $\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{n}{n-k}}\right)$.

• $k\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right)=n\left({\displaystyle \genfrac{}{}{0pt}{}{n-1}{k-1}}\right)$.

• $\left({\displaystyle \genfrac{}{}{0pt}{}{n+1}{k}}\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k-1}}\right)+\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right)$ (Pascal’s triangle).

• ${\displaystyle \sum _{k=0}^n}\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right)=2^n$.

• ${\displaystyle \sum _{k=0}^n}{\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right)}^2=\left({\displaystyle \genfrac{}{}{0pt}{}{2n}{n}}\right)$.

• ${(1+t)}^n={\displaystyle \sum _{k=0}^n}\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right)t^k$ (Binomial Theorem).

Proof 2.3.

a) Instead of selecting a subset of $k$ elements we could select the $n-k$ elements not in the set.
b) Suppose we want to count committees of $k$ people (out of $n$) with a designated chair. We can do so by either choosing first the $\left(\genfrac{}{}{0pt}{}{n}{k}\right)$ committees and then for each team the $k$ possible chairs out of the committee members. Or we choose first the $n$ possible chairs and then the remaining $k-1$ committee members out of the $n-1$ remaining persons.
c) Suppose that I am part of a group that contains $n+1$ persons and we want to determine subsets of this group that contain $k$ people. These either include me (and $k-1$ further persons from the $n$ others), or do not include me and thus $k$ from the $n$ other people.
d) We count the total number of subsets of a set with $n$ elements. Each subset can be described by a $0/1$ sequence of length $n$, indicating whether the $i$-th element is in the set.
e) Suppose we have $n$ men and $n$ women and we want to select groups of $n$ persons. This is the right hand side. The number of possibilities with exactly $k$ women is $\left(\genfrac{}{}{0pt}{}{n}{k}\right)\left(\genfrac{}{}{0pt}{}{n}{n-k}\right)={\left(\genfrac{}{}{0pt}{}{n}{k}\right)}^2$ by a). The left hand of the equation simply sums these over all possible $k$.
f) Clearly ${(1+t)}^n$ is a polynomial of degree $n$. The coefficient for $t^k$ gives the number of possibilities to choose the $t$-summand when multiplying out the product

$$(1+t)(1+t)\cdot \mathrm{\cdots }\cdot (1+t)$$

of $n$ factors so that there are $k$ such summands overall. This is simply the number of $k$-subsets, $\left(\genfrac{}{}{0pt}{}{n}{k}\right)$.

Prove the theorem using induction. Compare the effort. Which method gives you more insight?

3 Stirling’s Estimate

Since the factorial function is somewhat unhandy in estimates, it can be useful to have an approximation in terms of elementary functions. The most prominent of such estimates is given by Stirling’s formula. Our description follows [fellerstirling]:

Theorem 5.

$$n!\approx \sqrt{2\pi n}{\left(\frac{n}{e}\right)}^n\left(1+O\left(\frac{1}{n}\right)\right).$$ (1)

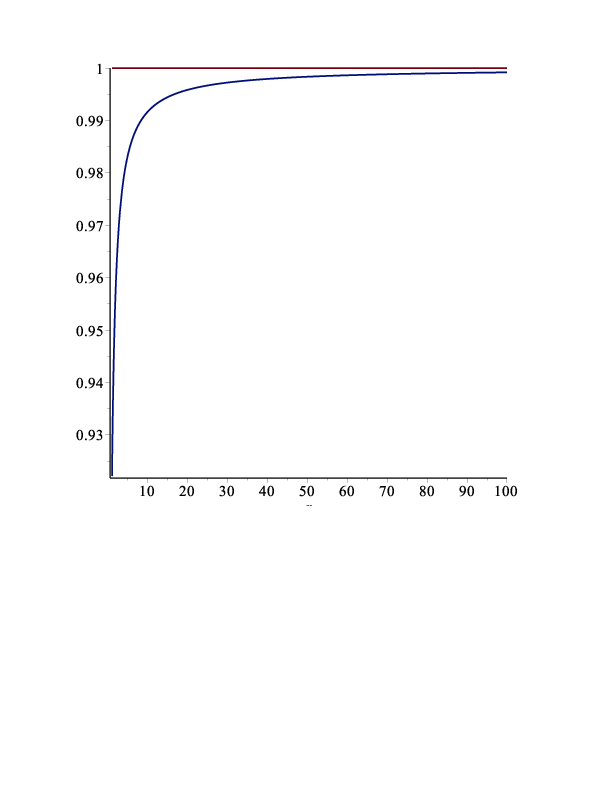
Here $1+O(1/n)$ means that the quotient of the estimate and the true value is bounded by $1\pm 1/n$, that is the relative error is $O(1/n)$. Figure 2 shows a plot of the ratio of the estimate to $n!$.

Figure 2: Plot of $\sqrt{2\pi n}{\left(\frac{n}{e}\right)}^n/n!$

Proof 3.1.

Consider the natural logarithm of the factorial:

$$\log (n!)=\log 1+\log 2+\mathrm{\cdots }+\log n$$

If we define a step function $L(x)=\log (\lfloor x+1/2\rfloor )$, we thus have that $\log (n!)$ is an integral of $L(x)$. We also know that

$$I(x)={\int }_0^x\log (t)𝑑t=x\log x-x.$$

We thus need to consider the integral over $L(x)-\log (x)$. To avoid divergence issues, we consider this in two parts. Let

$$a_k=\frac{1}{2}\log k-{\int }_{k-\frac{1}{2}}^k\log xdx={\int }_{k-\frac{1}{2}}^k\log (k/x)𝑑x,$$

and

$$b_k={\int }_k^{k+\frac{1}{2}}\log xdx-\frac{1}{2}\log k={\int }_k^{l+\frac{1}{2}}\log (x/k)𝑑x.$$

Then

$$S_n=a_1-b_1+a_2-b_2+\mathrm{\cdots }+a_n=\log n!-\frac{1}{2}\log n+I(n)-I(\frac{1}{2}).$$

A substitution gives

$$a_k={\int }_0^{\frac{1}{2}}\log \frac{1}{1-(t/k)}dt,b_k={\int }_0^{\frac{1}{2}}\log (1+t/k)𝑑t,$$

from which we see that $a_k>b_k>a_{k+1}>0$. By the Leibniz’ criterion thus $S_n$ converges to a value $S$ and we have that

$$\log n!-(n+\frac{1}{2})\log n+n\to S-I(\frac{1}{2}).$$

Taking the exponential function we get that

$$n!\to e^C\sqrt{n}{\left(\frac{n}{e}\right)}^n$$

with $C={\sum }_{k=1}^{\mathrm{\infty }}(a_k-b_k)-I(\frac{1}{2})$.

Using standard analysis techniques, one can now show that $e^C=\sqrt{2\pi }$; see [fellerstirling] for details. Alternatively, in concrete calculations, we could simply approximate the value to any accuracy desired.

The appearance of $e$ might seem surprising, but the following example shows that it arises naturally in this context:

Proposition 6.

The number $s_n$ of all sequences (of arbitrary length) without repetition that can be formed from $n$ objects is $\lfloor e\cdot n!\rfloor$.

We note that no sequence can have length more than $n!$, as this would require repetition.

Proof 3.2.

If we have a sequence of length $k$, there are ${(n)}_k=k!\left(\genfrac{}{}{0pt}{}{n}{k}\right)=\frac{n!}{(n-k)!}$ sequences of length $k$. Summing over all values of $n-k$ we get (with an index shift, replacing $k$ by $n-k$):

$$s_n=\sum _{k=0}^n\frac{n!}{k!}=n!\sum _{k=0}^n\frac{1}{k!}.$$

Using the Taylor series for $e^x$ we see that

$e\cdot n!-s_n$ $=$ ${\displaystyle \frac{1}{n+1}}+{\displaystyle \frac{1}{(n+1)(n+2)}}+\mathrm{\cdots }$

${\displaystyle \frac{1}{n+1}}+{\displaystyle \frac{1}{{(n+1)}^2}}+\mathrm{\cdots }$

$=$

This is an example (if we ignore language meaning) of the popular problem how many words could be formed from the letters of a given word, if no letters are duplicate.

If we allow duplicate letters the situation gets harder. For example, consider words (ignoring meaning) made from the letters of the word COLORADO. The letter O occurs thrice, the other five letters only once. If a word contains at most one O, the formula from above gives $\lfloor e\cdot 6!\rfloor ={\sum }_{k=0}^6\frac{6!}{k!}=720+720+360+120+30+5+1=1957$ such words.

For more than one O, the above formula can’t be used any longer, but we need to go back to summations. If the word contains two O, and $k$ other letters there are $\left(\genfrac{}{}{0pt}{}{5}{k}\right)$ options to select these letters and $(k+2)!/2$ possibility to arrange the letters (the denominator 2 making up for the fact that both O cannot be distinguished). Thus we get

$$\frac{2!}{2}+\frac{5\cdot 3!}{2}+\frac{10\cdot 4!}{2}+\frac{10\cdot 5!}{2}+\frac{5\cdot 6!}{2}+\frac{7!}{2}=1+15+120+600+1800+2520=5056$$

such words.

If the word contains three O, and $k$ other letters we get a similar formula, but with a cofactor $(k+3)!/6$, reflecting the $3!=6$ arrangements of the three O which yield the same word. We thus have

$$\frac{3!}{6}+\frac{5\cdot 4!}{6}+\frac{10\cdot 5!}{6}+\frac{10\cdot 6!}{6}+\frac{5\cdot 7!}{6}+\frac{8!}{6}=1+20+200+1200+4200+6720=12341$$

possibilities, summing up to $19354$ possibilities in total.

Lucky we do not live in MISSISSIPPI!

4 The Twelvefold Way

A generalization of counting sets and sequences is given by considering functions between finite sets. We shall consider functions $f:N\to X$ with $\left|N\right|=n$ and $\left|X\right|=x$. These functions could be arbitrary, injective, or surjective.

What does the concept of order (in)significant mean in this context? If the order is not significant, we actually only care about the set of values of a function, but not the values on particular elements. That is, all the elements of $N$ are equivalent, we call them indistinguishable or unlabeled (since labels will force objects to be different). Otherwise we talk about distinguishable or labeled objects.

Formally, we are counting equivalence classes of functions, in which two functions $f,g:N\to X$ are called $N$-equivalent, if there is a bijection $u:N\to N$ such that $f(u(a))=g(a)$ for all $a\in N$.

Similarly, we define an $X$-equivalence of function, calling s$f$ and $g$ equivalent, if there is $v:X\to X$ such that $v(f(a))=g(a)$ for all $a\in N$. If we say the elements of $X$ are indistinguishable, we count functions up to $X$-equivalence.

We can combine both equivalences to get even larger equivalence classes, which are the case of elements of both $N$ and $X$ being indistinguishable.

(The reader might feel this to be insufficiently stringent, or wonder about the case of different classes of equivalent objects. We will treat such situations in Section LABEL:polya under the framework of group actions.)

This setup ($N$ and $X$ distinguishable or not and functions being injective, surjective or neither) gives in total $3\cdot 2\cdot 2=12$ possible classes of functions. This set of counting problems is called the Twelvefold Way in [stanley1, Section 1.9] (and attributed there to Gian-Carlo Rota).

For each of the 12 categories, give an example of a concrete counting problem in common language. Say, we have $n$ balls and $x$ boxes (either of them might be labeled), and we might require that no box has more than one ball, or that every box contains at least one ball.

Say, we have $N=\{1,2\}$ and $X=\{a,b,c\}$. Then we have the following functions $N\to X$:

All functions:

There are 9 functions, namely (giving functions as sequences of values): $[a,a],[a,b],[a,c],[b,a],[b,b],[b,c],[c,a],[c,b],[c,c].$

Injective functions:

There are 6 functions, namely $[a,b],[a,c],[b,a],[b,c],[c,a],[c,b].$

Surjective functions:

There are no such functions, but there are 6 functions from $\{1,2,3\}$ to $\{a,b\}$, namely: $[a,a,b],[a,b,a],[a,b,b],[b,a,a],[b,a,b],[b,b,a].$

Up to permutation of $N$

So we consider only the sets of values, which gives 6 possibilities: $\{a,a\},\{a,b\},\{a,c\},\{b,b\},\{b,c\},\{c,c\}.$

Injective, up to permutation of $N$

The values need to be different, so 3 possibilities: $\{a,b\},\{a,c\},\{b,c\}.$

Surjective, up to permutation of $N$

There are no such functions, but there are 2 such functions from $\{1,2,3\}$ to $\{a,b\}$, namely: $[a,a,b],[a,b,b].$

Up to permutations of $X$

Since $\left|N\right|=2$, the question is just whether the two values are the same or not: $[a,a],[a,b].$

Injective, up to permutations of $X$

Here $[a,b]$ is the only such function.

Surjective, up to permutations of $X$

Again, no such function, but from $\{1,2,3\}$ to $\{a,b\}$ there are 3 such functions namely $[a,a,b],[a,b,a],[b,a,a].$

Up to permutations of $N$ and $X$

Again two possibilities, $[a,a],[a,b];$ but if $N=\{1,2,3\}$, there are three possibilities, namely $[a,a,a],[a,a,b],[a,b,c].$

Injective, up to permutations of $N$ and $X$

Again, $[a,b]$ is the only such function.

Surjective, up to permutations of $N$ and $X$

Again, no such function, but from $\{1,2,3\}$ to $\{a,b\}$ there is one, namely $[a,a,b]$.

We are now getting ready to give formulas for the number of functions in each class, depending only on $n$ and $x$. For this we introduce the following definitions. Determining closed formulae for these is not always easy, and will require further work in subsequent chapters.

A partition of a set $A$ is a collection $\{A_i\}$ of subsets (called parts or cells) $\mathrm{\varnothing }\ne A_i\subset A$ such that for all $i$:

• ${\displaystyle \bigcup _i}{A}_i=A$

• $A_i\cap A_j=\mathrm{\varnothing }$ for $j\ne i$.

Note that a partition of a set gives an equivalence relation and that any equivalence relation on a set defines a partition into equivalence classes.

Definition 7.

We denote the number of partitions of $\{1,\mathrm{\dots },n\}$ into $k$ (non-empty) parts by $S(n,k)$. It is called the Stirling number of the second kind OEIS A0082h7. The total number of partitions of $\{1,\mathrm{\dots },n\}$ is given by the Bell number OEIS A000110

$$B_n=\sum _{k=1}^{n}S(n,k).$$

There are $B_3=5$ partitions of the set $\{1,2,3\}$.

Again we might want to set $S(n,k)=0$ unless $1\le k\le n$.

We will give a formula for $S(n,k)$ in Lemma 6.1 and study $B(n)$ in section 1.

In some cases we shall care not which numbers are in which cells of a partition, but only the size of the cells. (That is, we only care about writing $n$ as a sum over an increasing sequence of positive integers: $n=1+3+4+6$.) Sometimes this is called an integer partition, a Young diagram, or a Ferrers diagram. Figure 3 shows these diagrams for partition $(1,3,4,6)$. In one style (called ”English”), the length of rows decrease as one goes downwards, in another (”French”) they do as one goes upwards.

We denote the number of partitions of $n$ into $k$ parts (ignoring which numbers are in which part) by $p_k(n)$, the total number of partitions by $p(n)$. OEIS A000041.

Figure 3: Partition $(1,3,4,6)$ as Ferrers diagram and Young diagrams, English and French style

Again we study the function $p(n)$ later, however here we shall not achieve a closed formula for the value.

We have $B_3=5$, but $p(3)=3$. This is because the three partitions $\{\{1\},\{2,3\}\}$, $\{\{2\},\{1,3\}\}$, $\{\{3\},\{1,2\}\}$ all have the same cell size pattern.

1 The twelvefold way theorem

We now extend the table of theorem 3:

Theorem 8.

if $N,X$ are finite sets with $\left|N\right|=n$ and $\left|X\right|=x$, the number of (equivalence classes of) functions $f:N\to X$ is given by the following table. (In the first two columns, d/i indicates whether elements are considered distinguishable or indistinguishable. The boxed numbers refer to the explanations in the proof.):

$N$	$X$	$f$ arbitrary	$f$ injective	$f$ surjective
d	d	${}_{}{}^{\text{1}}{x}^n$	${}_{}{}^{\text{2}}{(x)}_n$	${}_{}{}^{\text{3}}x!S(n,x)$
i	d	${}_{}{}^{\text{4}}\left(\left({\displaystyle \genfrac{}{}{0pt}{}{x}{n}}\right)\right)$	${}_{}{}^{\text{5}}\left({\displaystyle \genfrac{}{}{0pt}{}{x}{n}}\right)$	${}_{}{}^{\text{6}}\left({\displaystyle \genfrac{}{}{0pt}{}{n-1}{x-1}}\right)=\left(\left({\displaystyle \genfrac{}{}{0pt}{}{x}{n-x}}\right)\right)$
d	i	${}_{}{}^{\text{7}}{\displaystyle \sum _{k=1}^x}S(n,k)$		${}_{}{}^{\text{9}}S(n,x)$
i	i	${}_{}{}^{\text{10}}{\displaystyle \sum _{k=1}^x}{p}_k(n)$		${}_{}{}^{\text{12}}{p}_x(n)$

Proof 4.1.

If $N$ is distinguishable, we can simply write the elements of $N$ in a row and consider a function on $N$ as a sequence of values. In 1), we thus have sequences of length $n$ with $x$ possible values, in 2) such sequences without repetition, both formulas we already know.

If such a sequence takes exactly $x$ values, each value $f(n)$ can be taken to indicate the cell of a partition into $x$ parts, into which $n$ is placed. As we consider a partition as a set of parts, it does not distinguish the elements of $X$, that shows that the value in 9) has to be $S(n,x)$. If we distinguish the elements of $X$ we need to account for the $x!$ possible arrangements of cells, yielding the value in 3).

Similarly to 9), if we do not require $f$ to be surjective, the number of different values of $f$ gives us the number of parts. Up to $x$ different parts are possible, thus we need to add the values of the Stirling numbers.

To get 12) from 9) and 10) from 7) we notice that making the elements of $N$ indistinguishable simply means that we only care about the sizes of the parts, not which number is in which part. This means that the Stirling number $S(n,x)$ gets replaced by the partition (shape) count $p_x(n)$.

If we again start at 1) but now consider the elements of $N$ as indistinguishable, we go from sequences to sets. If $f$ is injective we have ordinary sets, in the general case multisets, and have already established the results of 4) and 5).

For 6), we interpret the $x$ distinct values of $f$ to separate the elements of $N$ into $x$ parts. This is a composition of $n$ into $x$ parts, for which the count has been established.

In 8) and 11), finally, injectivity demands that we assign all elements of $N$ to different values which is only possible if $n\le x$. As we do not distinguish the elements of $X$ it does not matter what the actual values are, thus there is only one such function up to equivalence.

Chapter 2 Recurrence and Generating Functions

There’s al-gebra. That’s like sums with letters. For…for people whose brains aren’t clever enough for numbers, see? Jingo
Terry Pratchett

Finding a closed formula for a combinatorial counting function can be hard. It often is much easier to establish a recursion, based on a reduction of the problem. Such a reduction often is the principal tool when constructing all objects in the respective class.

An easy example of such a situation is given by the number of partitions of $n$, given by the Bell numbers $B_n$:

Lemma 0.1.

For $n\ge 1$ we have:

$$B_n=\sum _{k=1}^n\left(\genfrac{}{}{0pt}{}{n-1}{k-1}\right)B_{n-k}$$

Proof 0.2.

Consider a partition of $\{1,\mathrm{\dots },n\}$. Being a partition, it must have $1$ in one cell. We group the partitions according to how many points are in the cell containing $1$. If there are $k$ elements in this cell, there are $\left(\genfrac{}{}{0pt}{}{n-1}{k-1}\right)$ options for the other points in this cell. And the rest of the partition is simply a partition of the remaining $n-k$ points.

1 Power Series – A touch of Calculus

A powerful technique for working with recurrence relations is that of generating functions. The definition is easy, for a counting function $f:{\mathbb{Z}}_{\ge 0}\to ℝ$ defined on the nonnegative integers we define the associated generating function as the power series

$$F(t)=\sum _{n=0}^{\mathrm{\infty }}{f}_n{t}^n\in ℝ[[t]]$$

Here $ℝ[[t]]$ is the ring of formal power series in $t$, that is the set of all formal sums ${\sum }_{n=0}^{\mathrm{\infty }}{a}_n{t}^n$ with $a_n\in ℝ$.

When writing down such objects, we ignore the question whether the series converges, i.e. whether $F$ can be interpreted as a function on a subset of the real numbers.

The reader interested in a rigorous, self-contained, presentation of the theory of formal power series, that does not require any reliance of results from analysis, can find it in [sambale2024].

Addition and multiplication are as one would expect: If $F(t)={\sum }_{n\ge 0}{f}_n{t}^n$ and $G(t)={\sum }_{n\ge 0}{g}_n{t}^n$ we define new power series $F+G$ and $F\cdot G$ by:

$(F+G)(t)$ $:=$ ${\displaystyle \sum _{n\ge 0}}(f_n+g_n)t^n$

$(F\cdot G)(t)$ $:=$ ${\displaystyle \sum _{n\ge 0}}\left({\displaystyle \sum _{a+b=n}}{f}_a{g}_b\right)t^n.$

With this arithmetic $R[[t]]$ becomes a commutative ring. (There is no convergence issue, as the sum over $a+b=n$ is always finite.)

We also define two operators, called differentiation and integration on $ℝ[[t]]$ by

$$\frac{\text{d}}{\text{d}t}\left(\sum _{n\ge 0}{a}_n{t}^n\right)=\sum _{n\ge 1}(n{a}_n)t^{n-1}$$

and

$$\int \left(\sum _{n\ge 0}{a}_n{t}^n\right)=\sum _{n\ge 0}\frac{a_n}{n+1}{t}^{n+1}$$

(with the integration constant is set as $0$).

Two power series are equal if and only if all coefficients are equal. An identity involving a power series as a variable is called a functional equation.

As a “shorthand”, pretending we knew nothing from Calculus (after all, we do not establish convergence), we define the following names for particular power series:

$\exp (t)$ $=$ ${\displaystyle \sum _{n\ge 0}}{\displaystyle \frac{t^n}{n!}}$

$\log (1+t)$ $=$ ${\displaystyle \sum _{n\ge 1}}{\displaystyle \frac{{(-1)}^{n-1}{t}^n}{n}}$

and note that the usual functional identities $\exp (a+b)=\exp (a)\exp (b)$, $\log (ab)=\log (a)+\log (b)$, $\log (\exp (t))=t$ and differential identities $\frac{\text{d}}{\text{d}t}\exp (t)=\exp (t)$, $\frac{\text{d}}{\text{d}t}\log (t)=1/t$ hold.

A telescoping argument shows that for $r\in ℝ$ we have that $(1-rt)\left({\sum }_n{r}^n{t}^n\right)=1$, that is we can use the geometric series identity

$$\sum _n{r}^n{t}^n=\frac{1}{1-rt}$$

to embed rational functions (whose denominators factor completely; this can be taken as given if we allow for complex coefficients) into the ring of power series.

For a real number $r$, we define the generalized binomial coefficient as:

$$\left(\genfrac{}{}{0pt}{}{r}{n}\right)=\frac{r(r-1)\mathrm{\cdots }(r-n+1)}{n!}$$

as well as a series representation of the $r$-th power:

$${(1+t)}^r=\sum _{n\ge 0}\left(\genfrac{}{}{0pt}{}{r}{n}\right)t^n.$$

For obvious reasons we call this definition the binomial formula. Note that for integral $r$ this agrees with the usual definition of exponents and binomial coefficients, so there is no conflict with the traditional definition of exponents.

We also notice that for arbitrary $r,s$ we have that ${(1+t)}^r{(1+t)}^s={(1+t)}^{r+s}$ and $\frac{\text{d}}{\text{d}t}{(1+t)}^r=r{(1+t)}^{r-1}$.

Up to this point, generating functions seem to be a formality for formalities sake. They however come into their own with the following observations: Operations on the entries of a sequence, relations amongst its entries (such as recursion), or a sequence having been built on top of other sequences often have natural analogues with generating functions. Recursive identities amongst a coefficient sequence then become functional equations or differential equations for the generating functions.

If these equations have solutions, known start values typically give uniqueness of the solution, and (assuming it converges in an open interval), its power series representation must be identical to the generating function. Methods from Analysis, such as Taylor’s theorem, then can be used to determine expressions for the terms of the sequence.

Before describing this more formally, let us look at a toy example:

We define a function recursively by setting $f_0=1$ and $f_{n+1}=2f_n$. (This recursion comes from the number of subsets of a set of cardinality $n$ – fix one element and distinguish between subsets containing this element and those that don’t.) The associated generating function is $F(t)={\sum }_{n\ge 0}{f}_n{t}^n$. We now observe that

$$2tF(t)=\sum _{n\ge 0}2f_n{t}^{n+1}=\sum _{n\ge 0}{f}_{n+1}{t}^{n+1}=F(t)-1.$$

We solve this functional equation as

$$F(t)=\frac{1}{1-2t}$$

and (geometric series!) obtain the power series representation

$$F(t)=\sum _{n\ge 0}{2}^n{t}^n.$$

this allows us to conclude that $f_n=2^n$, solving the recursion (and giving the combinatorial result (which we knew already by another method) that a set of cardinality $n$ has $2^n$ subsets.)

1 Operations on Generating Functions

To prepare us for working with generating functions, let’s look in more detail on what generating function operations do with the coefficients.

For this, assume that $f_n$ and $g_n$ are sequences, associated to generating functions $F(t)={\sum }_n{f}_n{t}^n$ and $G(t)={\sum }_n{g}_n{t}^n$, respectively.

We start with basic linearity. $\lambda F(t)+G(t)$ is the generating function associated to the sequence $\lambda f_n+g_n$. The case $\lambda =1$ is sometimes called the sum rule, describing the case that $f$ and $g$ count the cardinality of disjoint sets and $f_n+g_n$ the cardinality of their unions.

Shifting

Shifting the indices corresponds to multiplication by (positive or negative) powers of $t$.

Differentiation

If $F(t)={\sum }_{i\ge 0}{f}_i{t}^i$, the derivative of $F(t)$ corresponds to the sequence $s_n=(n+1)f_{n+1}$. This will allow for coefficients that also depend on the index position. This can often be used effectively together with shifts. For example, starting with the sequence $f_n=1$, it corresponds (geometric series) to the generating function $\frac{1}{1-t}$. Its derivative, $\frac{1}{{(1-t)}^2}$ thus corresponds to the sequence $1,2,3,4,\mathrm{\dots }$. Thus $\frac{t}{{(1-t)}^2}$ corresponds to the sequence $0,1,2,3,\mathrm{\dots }$. If we take a further derivative, we multiply each coefficient with its index position and shift back, resulting in a sequence of squares $1,4,9,16,\mathrm{\dots }$. The associated generating function will be the derivative function $\frac{1+t}{{(1-t)}^3}$. We can shift once more to get the sequence $s_n=n^2$, associated to the generating function $\frac{t(1+t)}{{(1-t)}^3}$.

Products

If we define a new sequence as sum of terms whose indices add up to a given value (this is sometimes called convolution):

$$c_n=f_0{g}_n+f_1{g}_{n-1}+f_2{g}_{n-2}+\mathrm{\cdots }+f_n{g}_0$$

its generating function will be $F(t)\cdot G(t)$. This is called the product rule.

One particular case of this is the summation rule: Suppose we define one sequence by summing over another: $c_n={\sum }_{i=0}^n{f}_i$. We can interpret this as convolution with the constant sequence $g_i=1$, whose generating function is $\frac{1}{1-t}$. The generating function for the summatory sequence thus is $C(t)=\frac{F(t)}{1-t}$.

Continuing the previous example, the sequence $s_n={\sum }_{i=0}^n{i}^2$ thus has the generating function $S(t)=\frac{t(1+t)}{{(1-t)}^4}$.

The standard reference for generating functions is [generatingfunctionology]. The book [concrete] has a dedicated chapter, written on the level of an (advanced) undergraduate textbook.

We now make use of these tools by looking at general tools to find closed-form expressions for recursively defined sequences.

2 Linear recursion with constant coefficients

Then, at the age of forty, you sit,
theologians without Jehovah,
hairless and sick of altitude,
in weathered suits,
before an empty desk,
burned out, oh Fibonacci,
oh Kummer¹, oh Gödel, oh Mandelbrot
in the purgatory of recursion. ¹  also means: “grief”xxxxxxxxxxxxxx

Dann, mit vierzig, sitzt ihr,

o Theologen ohne Jehova,

haarlos und höhenkrank

in verwitterten Anzügen

vor dem leeren Schreibtisch,

ausgebrannt, o Fibonacci,

o Kummer, o Gödel, o Mandelbrot,

im Fegefeuer der Rekursion. Die Mathematiker

Hans Magnus Enzensberger

Suppose that $f_n$ satisfies a recursion of the form

$$f_n=a_1{f}_{n-1}+a_2{f}_{n-2}+\mathrm{\cdots }+a_k{f}_{n-k}.$$

That is, there is a fixed number of recursion terms and each term is just a scalar multiple of a prior value (we shall see below that easy cases of index dependence also can be treated this way). We also assume that $k$ initial values $f_0,\mathrm{\cdots },f_{k-1}$ have been established.

The most prominent case of this are clearly the Fibonacci numbers OEIS A000045 with $k=2$, recursion $f_n=f_{n-1}+f_{n-2}$ and initial values $f_0=f_1=1$. We shall use these as an example.

Step 1: Get the functional equation

Using the recursion, expand the coefficient $f_n$ in the generating function $F(t)={\sum }_n{f}_n{t}^n$ with terms of lower index. Note that for the recursion does not hold, you will need to look at the initial values to see whether the given formula suffices, or if you need to add explicit multiples of powers of $t$ to get equality.

Separate summands into different sums, factor out powers of $t$ to get $f_n$ combined with $t^n$.

Replace all expressions $\sum f_n{t}^n$ back with the generating function $F(t)$. The whole expression also must be equal to $F(t)$, this is the functional equation.

in the case of the Fibonacci numbers, the recursion is $f_n=f_{n-1}+f_{n-2}$ for $n>1$. Thus we get, using the initial values $f_0=f_1=1$, that

${\displaystyle \sum _{n\ge 0}}{f}_n{t}^n$ $=$ ${\displaystyle \sum _{n>1}}\left(f_{n-1}{t}^n+f_{n-2}{t}^n\right)+f_{1}t+f_0$

$=$ ${\displaystyle \sum _{n>1}}{f}_{n-1}{t}^n+{\displaystyle \sum _{n>1}}{f}_{n-2}{t}^n+t+1$

$=$ $t{\displaystyle \sum _{n>1}}{f}_{n-1}{t}^{n-1}+t^2{\displaystyle \sum _{n>1}}{f}_{n-2}{t}^{n-2}+t+1$

$=$ $t{\displaystyle \sum _{n>0}}{f}_n{t}^n+t^2{\displaystyle \sum _{n\ge 0}}{f}_n{t}^n+t+1$

$=$ $t({\displaystyle \sum _{n\ge 0}}{f}_n{t}^n-f_0)+t^2{\displaystyle \sum _{n\ge 0}}{f}_n{t}^n+t+1$

$=$ $t\cdot F(t)-t\cdot f_0+t^{2}F(t)+t+1=t\cdot F(t)+t^{2}F(t)+1.$

The functional equation is thus $F(t)=t\cdot F(t)+t^{2}F(t)+1$, respectively $F(t)(1-t-t^2)=1$.

Step 2: Partial Fractions

We can solve the functional equation to express $F(t)$ as a rational function in $t$. (This is possible, because the functional equation will be a linear polynomial in $F(t)$.) Then, using partial fractions (Calculus 2), we can write this as a sum of terms of the form ${\displaystyle \frac{a_i}{{(t-{\alpha }_i)}^{e_i}}}$.

We solve the functional equation and obtain $F(t)={\displaystyle \frac{1}{1-t-t^2}}$. For a partial fraction decomposition, let $\alpha =\frac{-1+\sqrt{5}}{2}$, $\beta =\frac{-1-\sqrt{5}}{2}$, be the roots of the denominator polynomial $1-t-t^2=0$. Then

$$F(t)=\frac{1}{1-t-t^2}=\frac{a}{t-\alpha }+\frac{b}{t-\beta }$$

We solve this as $a=-1/\sqrt{5}$, $b=1/\sqrt{(}5)$.

Step 3: Use known power series to express each summand as a power series

The geometric series gives us that

$$\frac{a}{t-\alpha }=\sum _{n\ge 0}\frac{-a}{{\alpha }^{n+1}}{t}^n$$

If there are multiple roots, denominators could arise in powers. For this we notice that

$$\frac{1}{{(t-\alpha )}^2}=\sum _{n\ge 0}\frac{(n+1)}{{\alpha }^{n+2}}{t}^n$$

and for an integer $c\ge 1$ that

$$\frac{1}{{(t-1)}^c}=-1^c\sum _{n\ge 0}\left(\genfrac{}{}{0pt}{}{c+n-1}{n}\right)t^n$$

Using these formulae, we can write each summand of the partial fraction decomposition as an infinite series.

In the example we get

$F(t)$ $=$ ${\displaystyle \frac{-1}{\sqrt{5}}}{\displaystyle \frac{1}{t-\alpha }}+{\displaystyle \frac{1}{\sqrt{5}}}{\displaystyle \frac{1}{t-\beta }}$

$=$ ${\displaystyle \frac{-1}{\sqrt{5}}}{\displaystyle \sum _{n\ge 0}}{\displaystyle \frac{-1}{{\alpha }^{n+1}}}{t}^n+{\displaystyle \frac{1}{\sqrt{5}}}{\displaystyle \sum _{n\ge 0}}{\displaystyle \frac{-1}{{\beta }^{n+1}}}{t}^n$

Step 4: Combine to one sum, and read off coefficients

We now take this (unique!) power series expression and read off the coefficients. The coefficient of $t^n$ will be $f_n$, which gives us an explicit formula.

Continuing the calculation above, we get

$$F(t)=\sum _{n\ge 0}\left(\frac{1}{\sqrt{5}\cdot {\alpha }^{n+1}}+\frac{-1}{\sqrt{5}\cdot {\beta }^{n+1}}\right)t^n$$

and thus a closed formula for the Fibonacci numbers:

$f_n$ $=$ ${\displaystyle \frac{1}{\sqrt{5}\cdot {\alpha }^{n+1}}}+{\displaystyle \frac{-1}{\sqrt{5}\cdot {\beta }^{n+1}}}$

$=$ ${\displaystyle \frac{1}{\sqrt{5}\cdot {\left(\frac{-1+\sqrt{5}}{2}\right)}^{n+1}}}+{\displaystyle \frac{-1}{\sqrt{5}\cdot {\left(\frac{-1-\sqrt{5}}{2}\right)}^{n+1}}}$

$=$ ${\displaystyle \frac{1}{\sqrt{5}}}\left({\left({\displaystyle \frac{2}{\sqrt{5}-1}}\right)}^{n+1}+{\left({\displaystyle \frac{2}{\sqrt{5}+1}}\right)}^{n+1}\right)$

We notice that ${\displaystyle \frac{2}{\sqrt{5}-1}}>{\displaystyle \frac{2}{\sqrt{5}+1}}>0$, thus asymptotically, as $n\to \mathrm{\infty }$:

$$f_{n+1}/f_n=\frac{2}{\sqrt{5}-1}=\varphi \approx 1.618$$

the value of the golden ratio.

1 Another example

We try another example. Take the (somewhat random, but involving an index-dependent term that makes it more complicated) recursion given by

$g_0$ $=$ $g_1=1$

$g_n$ $=$ $g_{n-1}+2\cdot g_{n-2}+{(-1)}^n,\text{for }n\ge 2$

We get for the generating function

$G(t)$ $=$ ${\displaystyle \sum _n}{g}_n{t}^n={\displaystyle \sum _{n\ge 1}}{g}_{n-1}{t}^n+2{\displaystyle \sum _{n\ge 2}}{g}_{n-2}{t}^n+{\displaystyle \sum _{n\ge 0}}{(-1)}^n{t}^n+t$

$=$ $tG(t)+2t^{2}G(t)+{\displaystyle \frac{1}{1+t}}+t.$

(you should verify that the addition of $t$ was all that was required to resolve the initial value settings.)

We solve this functional equation as

$$G(t)=\frac{1+t+t^2}{(1-2t){(1+t)}^2}$$

and get (e.g. in Wolfram Alpha: partial fractions (1+t+t^2)/(1-2*t)/(1+t)^2) the partial fraction decomposition

$$G(t)=\frac{-7}{18(t-\frac{1}{2})}-\frac{1}{9(t+1)}+\frac{1}{3{(t+1)}^2}.$$

an can read off the power series representation

$G(t)$ $=$ ${\displaystyle \frac{7}{18}}{\displaystyle \sum _n}{2}^{n+1}{t}^n+{\displaystyle \frac{1}{9}}{\displaystyle \sum _n}{(-1)}^{n+1}{t}^n+{\displaystyle \frac{1}{3}}{\displaystyle \sum _n}-1^n(n+1)t^n$

$=$ ${\displaystyle \sum _n}\left({\displaystyle \frac{7}{9}}{2}^n-{\displaystyle \frac{1}{9}}{(-1)}^n+{\displaystyle \frac{1}{3}}{(-1)}^n(n+1)\right)t^n$

$=$ ${\displaystyle \sum _n}\left({\displaystyle \frac{7}{9}}{2}^n+\left({\displaystyle \frac{1}{3}}n+{\displaystyle \frac{2}{9}}\right){(-1)}^n\right)t^n,$

solving the recursion as $g_n=\frac{7}{9}{2}^n+\left(\frac{1}{3}n+\frac{2}{9}\right){(-1)}^n$.

3 Nested Recursions: Domino Tilings

The Domino Theory had become conventional wisdom and was rarely challenged. Diplomacy
Henry Kissinger

We now consider a number of problems that stem from counting arrangements of objects in the plane. While these counts themselves are not of deep importance, they produce nice examples of recursions.

Figure 1: A $2\times 10$ domino tiling

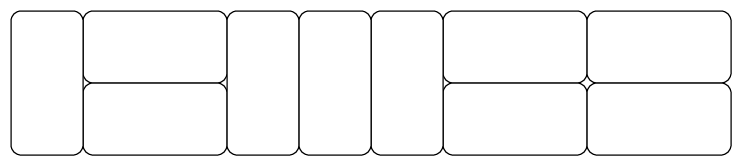
Suppose we have tiles that have dimensions $1\times 2$ (in your favorite units) and we want to tile a corridor. Let $d_n$ be the number of possible tilings of a corridor that has dimensions $2\times n$. We can start on the left with a vertical domino (thus leaving to the right of it a tiling of a corridor of length $n-1$) or with two horizontal dominos (leaving to the right of it a corridor of length $n-2$). this gives us the recursion

$$d_n=d_{n-1}+d_{n-2},n>1,$$

with $d_1=1$ and $d_2=2$ (and thus $d_0=1$ to fit the recursion). This is again the Fibonacci numbers we have already worked out.

If we assume that the tiles are not symmetric, there are actually two ways to place a horizontal tile and itwo ways to place a vertical tile. We thus get a recursion with different coefficients,

$$d_n=2d_{n-1}+4d_{n-2},n>1$$

with $d_1=2$, $d_2=8$ (and thus $d_0=1$).

1 Multiple recursions

We go back to the assumption of symmetric tiles, but expand the corridor to dimensions $3\times n$. The recursion approach now seems to be problematic – it is possible to have patterns or arbitrary length that do not reduce to a shorter length, see figure 2.

Figure 2: A tiling pattern that has no vertical cut

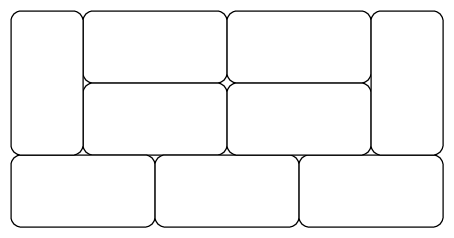
We thus instead look only at the right end of the tiling and argue that every tiling has to end with one of the three patterns depicted in the top row of figure 3.

Removing these end pieces either produces a tiling of length $n-2$, or a tiling of length $n$ in which the top (or bottom) right corner is missing. We thus introduce a count $e_n$ for tilings of length $n$ with the top right corner missing, the count for the bottom right corner missing will by symmetry be the same. The three possible end cases thus give us the recursion

$$d_n=d_{n-2}+2\cdot e_{n-1}$$

Figure 3: Variants for a $3\times n$ tiling

Since we also need no know the values of $e_n$, we build a recursive formula for them as well. Consider a tiling with the top right corner missing. It’s right end must be a vertical tile or two horizontal tiles. In this second case there also will have to be a further horizontal tile in the top row; the ends thus look as in the bottom row of figure 3.

This gives us the recursion

$$e_n=d_{n-1}+e_{n-2}$$

We use the initial values $d_0=1$, $d_1=0$, $d_2=3$, $e_0=0$, $e_1=1$, and thus get the following identities for the associate generating functions

$D(t)$ $=$ ${\displaystyle \sum _n}{d}_n{t}^n={\displaystyle \sum _{n>1}}\left(d_{n-2}+2e_{n-1}\right)t^n+d_0+d_{1}t$

$=$ $t^2{\displaystyle \sum _{n>1}}{d}_{n-2}{t}^{n-2}+2t{\displaystyle \sum _{n>1}}{e}_{n-1}{t}^{n-1}+1$

$=$ $t^2{\displaystyle \sum _{n\ge 0}}{d}_n{t}^n+2t({\displaystyle \sum _{n\ge 0}}{e}_n{t}^n-e_0{t}^0)+1$

$=$ $t^{2}D(t)+2tE(t)+1$

and

$E(t)$ $=$ ${\displaystyle \sum _n}{e}_n{t}^n={\displaystyle \sum _{n>1}}\left(d_{n-1}+e_{n-2}\right)t^n+e_0+e_{1}t$

$=$ $t(D(t)-d_0)+t^{2}E(t)+t=tD(t)+t^{2}E(t)$

We solve this second equation as

$$E(t)=\frac{t}{1-t^2}D(t)$$

and substitute into the first equation, obtaining the functional equation

$$D(t)=t^{2}D(t)+\frac{2t^2}{1-t^2}D(t)+1$$

which we solve for

$$D(t)=\frac{1-t^2}{1-4t^2+t^4}$$

This is a function in $t^2$, indicating that $d_n=0$ for odd $n$ (indeed, this must be, as in this case $3\times n$ is odd and cannot be tiled with tiles of area $2$). We thus can consider instead the function

$$R(t)=\frac{1-t}{1-4t+t^2}=\sum _n{r}_n{t}^n$$

with $d_{2n}=r_n$. Partial fraction decomposition, geometric series, and final collection of coefficients gives us the formula

$$d_{2n}=r_n=\frac{{(2+\sqrt{3})}^n}{3-\sqrt{3}}+\frac{{(2-\sqrt{3})}^n}{3+\sqrt{3}}$$

and the sequence of $r_n$ given by OEIS A001835

$$1,3,11,41,153,571,2131,7953,29681,110771,413403,\mathrm{\dots }$$

If we consider wider corridors the recursions become more complicated. It is therefore somewhat surprising that it is possible to give a general formula for the number of ways of tiling an $m\times n$ rectangle with dominoes. According to [temperleyfisher], it is

$$\prod _{j=1}^{\lfloor \frac{m}{2}\rfloor }\prod _{k=1}^{\lfloor \frac{n}{2}\rfloor }\left(4{\cos }^2\frac{\pi j}{m+1}+4{\cos }^2\frac{\pi k}{n+1}\right),$$

but its derivation is beyond the scope of this course.

4 Catalan Numbers

The induction I used was pretty tedious, but I do not doubt that this result could be obtained much easier. Concerning the progression of the numbers 1, 2, 5, 14, 42, 132, etc. …

Die Induction aber, so ich gebraucht, war ziemlich mühsam, doch zweifle ich nicht, dass diese Sach nicht sollte weit leichter entwickelt werden können. Ueber die Progression der Zahlen 1, 2, 5, 14, 42, 132, etc. … Letter to Goldbach

September 4, 1751

Leonard Euler

Next, we look at an example of a recursion which is not linear; we also use what is essentially the product rule:

Definition 9.

The $n$-th Catalan number $C_n$ OEIS A000108 is defined as the number of different ways a sum of $n+1$ variables can be evaluated by inserting parentheses.

We have $C_0=C_1=1$, $C_2=2$: $(a+b)+c$ and $a+(b+c)$, and $C_3=5$:

$$\begin{array}{c}((a+b)+c)+d\\ (a+(b+c))+d\\ a+((b+c)+d)\\ a+(b+(c+d))\\ (a+b)+(c+d)\end{array}$$

To get a recursion, consider the position of the “outermost” addition: suppose it is after $k+1$ of the variables have been encountered. On its left side is a parenthesized expression in $k+1$ variables, on the ride side is an expression in $(n+1)-(k+1)=n-k$ variables. We thus get the recursion

$$C_n=\sum _{k=0}^{n-1}{C}_k{C}_{n-k-1},\text{if }n>0\text{, }{C}_0=1.$$

in which we sum over the products of lower terms.

This is basically the pattern of the product rule, just shifted by one.

We thus get the functional equation

$$𝒞(t)=t\cdot 𝒞{(t)}^2+1.$$

(which is easiest seen by writing out the expression for $t𝒞{(t)}^2$ and collecting terms). The factor $t$ is due to the way we index and 1 is due to initial values.

This is a quadratic equation in $𝒞(t)$ and yields the solution

$$𝒞(t)=\frac{1-\sqrt{1-4t}}{2t}.$$

The branch of the root was chosen so that the function has a limit, namely the value of $C_0$, at $t\to 0$. (The other branch yields a singularity, see Figure 4.)

Figure 4: The two branches of $\frac{1\pm \sqrt{1-4t}}{2t}$

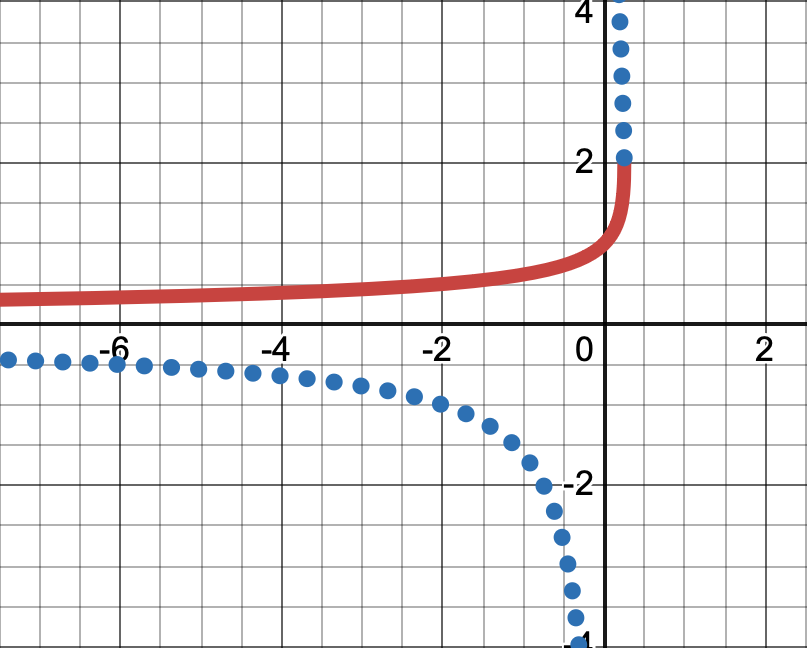
The binomial series gives

$$\sqrt{1-4t}=\sum _{k\ge 0}\left(\genfrac{}{}{0pt}{}{1/2}{k}\right){(-4t)}^k.=1+\sum _{k\ge 1}\left(\genfrac{}{}{0pt}{}{1/2}{k}\right){(-4t)}^k.$$

We also observe that

$\left({\displaystyle \genfrac{}{}{0pt}{}{1/2}{k}}\right){(-4t)}^k$ $=$ ${\displaystyle \frac{\frac{1}{2}\cdot \frac{-1}{2}\cdot \frac{-3}{2}\mathrm{\cdots }\frac{3-2k}{2}}{k!}}{(-1)}^k{2}^{2k}{t}^k$

$=$ ${\displaystyle \frac{{(-1)}^{k-1}(2k-3)(2k-5)\mathrm{\cdots }}{2^{k}k!}}{(-1)}^k{2}^{2k}{t}^k\text{set }n=k-1$

$=$ $-{\displaystyle \frac{2^{n+1}(2n-1)(2n-3)\mathrm{\cdots }}{(n+1)!}}{t}^{n+1}$

$=$ $-{\displaystyle \frac{(2n-1)(2n-3)\mathrm{\cdots }}{(n+1)!}}{2}^{n+1}{t}^{n+1}$

$=$ $-{\displaystyle \frac{2(2n)!}{(n+1)!n!}}{t}^{n+1}=-{\displaystyle \frac{2}{n+1}}\left({\displaystyle \genfrac{}{}{0pt}{}{2n}{n}}\right)t^{n+1}.$

Therefore

$$\frac{1-\sqrt{1-4t}}{2t}=\sum _{n\ge 0}\frac{1}{n+1}\left(\genfrac{}{}{0pt}{}{2n}{n}\right)t^n,$$

which shows that

$$C_n=\left(\genfrac{}{}{0pt}{}{2n}{n}\right)\frac{1}{n+1}=\frac{(2n)!}{n!(n+1)!}=\left(\genfrac{}{}{0pt}{}{2n}{n}\right)-\left(\genfrac{}{}{0pt}{}{2n}{n-1}\right).$$

Catalan numbers have many other combinatorial interpretations, and we shall encounter some in the exercises. Exercise 6.19 in [stanley2] (and its algebraic continuation 6.25, as well as an online supplement) contain hundreds of combinatorial interpretations.

5 Index-dependent coefficients and exponential generating functions

A recursion does not necessarily have constant coefficient, but might have a coefficient that is a polynomial in $n$. In this situation we can use (formal) differentiation, which will convert a term $f_n{t}^n$ into $n{f}_n{t}^{n-1}$. The second derivative will give a term $n(n-1)f_n{t}^{n-2}$; first and second derivative thus allow us to construct a coefficient $n^2{f}_n$ and so on for higher order polynomials.

The functional equation for the generating function then becomes a differential equation, and we might hope that a solution for it can be found in the extensive literature on differential equations.

Alternatively, (using the special form of derivatives for a typical summand), such a situation often can be translated immediately to a generating function by using the power series

$$\frac{1}{{(1-t)}^{k+1}}=\sum _n\left(\genfrac{}{}{0pt}{}{n+k}{n}\right)t^n.$$

For an example of variable coefficients, we take the case of counting derangements OEIS A000166, that is permutations that leave no point fixed. We denote by $d_n$ the number of derangements on $\{1,\mathrm{\dots },n\}$.

To build a recursion formula, suppose that $\pi$ is a derangement on $\{1,\mathrm{\dots },n\}$. Then . We now distinguish two cases, depending on how $i$ is mapped by $n$:

a) If $i^{\pi }=n$, then $\pi$ swaps $i$ and $n$ and is a derangement of the remaining $n-2$ points, thus there are $d_{n-2}$ derangements that swap $i$ and $n$. As there are $n-1$ choices for $i$, there are $(n-1)d_{n-2}$ derangements that swap $n$ with a smaller point.

b) Suppose there is $j\ne i$ such that $j^{\pi }=n$. In this case we can “bend” $\pi$ into another permutation $\psi$, by setting

We notice that $\psi$ is a derangement of the points $\{1,\mathrm{\dots },n-1\}$.

Vice versa, if $\psi$ is a derangement on $\{1,\mathrm{\dots },n-1\}$, and we choose a point , we can define $\pi$ on $\{1,\mathrm{\dots },n\}$ by

We again notice that $\pi$ is a derangement, and that different choices of $\psi$ and $i$ result in different $\pi$’s. Furthermore, the two constructions are mutually inverse, that is every derangement that is not in class a) is obtained by this construction.

There are $d_{n-1}$ possible derangements $\psi$ and $n-1$ choices for $j$, so there are $(n-1)d_{n-1}$ derangements in this second class.

We thus obtain a recursion

$$d_n=(n-1)\left(d_{n-1}+d_{n-2}\right)$$

and hand-calculate the initial values $d_0=1$ and $d_1=0$.

From this recursion we could now construct a differential equation for the generating function of $d_n$, but there is a problem: Because of the factor $n$ in the recursion, the values $d_n$ grow roughly like $n!$. The resulting series thus will have convergence radius $0$, making it unlikely that a function satisfying this differential equation can be found in the literature.

We therefore introduce the exponential generating function which is defined simply by dividing the $i$-th coefficient by a factor of $i!$, thus keeping coefficient growth bounded.

In our example, we get

$$D(t)=\sum _n\frac{d_n}{n!}{t}^n$$

and thus

$$\frac{\text{d}}{\text{d}t}D(t)=\sum _{n\ge 1}\frac{n\cdot d_n}{n!}{t}^{n-1}=\sum _{n\ge 1}\frac{d_n}{(n-1)!}{t}^{n-1}=\sum _{n\ge 0}\frac{d_{n+1}}{n!}{t}^n.$$

We also have

$t\cdot D(t)$ $=$ ${\displaystyle \sum _{n\ge 0}}{d}_n{\displaystyle \frac{t^{n+1}}{n!}}={\displaystyle \sum _{n\ge 0}}(n+1)d_n{\displaystyle \frac{t^{n+1}}{(n+1)!}}$

$=$ ${\displaystyle \sum _{n\ge 1}}n\cdot d_{n-1}{\displaystyle \frac{t^n}{n!}}={\displaystyle \sum _{n\ge 0}}n\cdot d_{n-1}{\displaystyle \frac{t^n}{n!}}$

$t\cdot D^{\prime }(t)$ $=$ ${\displaystyle \sum _{n\ge 0}}{\displaystyle \frac{n\cdot d_n}{n!}}{t}^n$

From this, the recursion (written as $d_{n+1}=n(d_n+d_{n-1})$) gives:

$t\cdot D(t)+t\cdot D^{\prime }(t)$ $=$ ${\displaystyle \sum _{n\ge 0}}\left(n\cdot d_{n-1}+n\cdot d_n\right){\displaystyle \frac{t^n}{n!}}$

$=$ ${\displaystyle \sum _{n\ge 0}}{d}_{n+1}{\displaystyle \frac{t^n}{n!}}=D^{\prime }(t),$

and thus the separable differential equation

$$\frac{D^{\prime }(t)}{D(t)}=\frac{t}{1-t}.$$

with $D(0)=d_0=1$.

Standard techniques from Calculus give the solution

$$D(t)=\frac{e^{-t}}{1-t}.$$

of this differential equation. Looking up this function for Taylor coefficients (respectively determining the formula by induction) shows that

$$D(t)=\sum _{n\ge 0}\left(\sum _{i=0}^n\frac{{(-1)}^i}{i!}\right)t^n$$

and thus (introducing a factor $n!$ to make up for the denominator in the generating function) that

$$d_n=n!\left(\sum _{i=0}^n\frac{{(-1)}^i}{i!}\right).$$

This is $n!$ ,multiplied with a Taylor approximation of $e^{-1}$. Indeed, if we consider the difference to $n!e^{-1}$, the alternating series gives, for $n\ge 1$:

$\left|d_n-{\displaystyle \frac{n!}{e}}\right|$ $=$ $n!\left|{\displaystyle \sum _{i=n+1}^{\mathrm{\infty }}}{\displaystyle \frac{{(-1)}^i}{i!}}\right|$

$n!\left|{\displaystyle \frac{{(-1)}^{n+1}}{(n+1)!}}\right|={\displaystyle \frac{1}{n+1}}\le {\displaystyle \frac{1}{2}}$

We have proven:

Lemma 5.1.

$d_n$ is the integer closest to $n!/e$.

That is asymptotically, if we put letters into envelopes, the probability is $1/e$ that no letter is in the correct envelope.

6 The product rule, revisited

Exponential generating functions have one more trick up their sleeve, arguably their most important contribution. For this, let us return to the product rule. It corresponds to the situation that the objects of a certain “weight” can be described in terms of combining objects of lower weights (that sum up to the desired weight) in all possible ways.

This splitting-up however only considers the number of (sub)objects in each part, not which particular ones are in each part. In other words, we consider the constituent objects as indistinguishable.

Suppose now, however, that we are counting objects whose parts have identifying labels. In the example of the Catalan numbers this would be for example, if we cared not only about the parentheses placement, but also about the symbols we add, that is $(a+b)+c$ would be different from $(c+a)+b$.

In such a situation, the recursion formula must, for each $k$, account for which $k$ elements are chosen to be in the “left side”, with the rest being in the“right side”. Every combination is possible. That is, the recursion becomes:

$$d_n=\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)a_k{b}_{n-k}.$$

We can write this as

$$\frac{d_n}{n!}=\sum _{k=0}^n\frac{a_k}{k!}\frac{b_{n-k}}{(n-k)!},$$

which is the formula for multiplication of the exponential generating functions!

Let us look at this in a pathetic example, the number of functions from $N=\{1,\mathrm{\dots },n\}$ to $\{1,\mathrm{\dots },r\}$ (which we know already well as $r^n$).

Let $a_n$ count the number of constant functions on an $n$-element set, that is $a_n=1$. The associated exponential generating function thus is

$$A(t)=\sum _n\frac{t^n}{n!}=\exp (t)$$

(which, incidentally, shows why these are called “exponential” generating functions).

If we take an arbitrary function $f$ on $N$, we can partition $N$ into $r$ (possibly empty) sets $N_1,\mathrm{\dots },N_r$, such that $f$ is constant on $N_i$ and the $N_i$ are maximal with this property.

We get all possible functions $f$ by combining constant functions on the possible $N_i$’s for all possible partitions of $N$. Note that the ordering of the partitions is significant – they indicate the actual values.

We are thus exactly in the situation described, and get as exponential generating function (start with $r=2$, then use induction for larger $r$) the $r$-fold product of the exponential generating functions for the number of constant functions:

$$D(t)=\underset{r\text{ factors}}{\underbrace{\exp (t)\cdot \mathrm{\cdots }\exp (t)}}=\exp (rt)$$

The coefficient for $t^n$ in the power series for $\exp (rt)$ is $\frac{r^n}{n!}$, and hence the counting function is $r^n$, as expected.

1 Bell Numbers

$${\int }_1^{\sqrt[3]{3}}{z}^2𝑑z\times \cos \frac{3\pi }{9}=\log (\sqrt[3]{e})$$

The integral $z$-squared d$z$,
From one to the cube root of three,
Times the cosine,
Of three pi over nine
Equals log of the cube root of e. Anon.

We try this approach next to obtain an exponential generating function for the Bell numbers (though not a closed form expression for its coefficients):

Recall that the Bell numbers $B_n$ give the total number of partitions of $\{1,\mathrm{\dots },n\}$ and satisfy (Lemma 0.1) the recursion:

$$B_n=\sum _{k=1}^n\left(\genfrac{}{}{0pt}{}{n-1}{k-1}\right)B_{n-k}=\sum _{k=0}^{n-1}\left(\genfrac{}{}{0pt}{}{n-1}{k}\right)B_{n-1-k}$$

In light of the product rule, we insert a factor 1 and write this (after reindexing) as

$$B_{n+1}=\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)1\cdot B_{n-k}$$

and thus

$$\sum _n\frac{B_{n+1}}{n!}{t}^n=\sum _t\left(\sum _{k=0}^n\frac{1}{k!}\cdot \frac{B_{n-k}}{(n-k)!}\right)t^n$$

If we denote the exponential generating function of the $B_n$ by $F(t)={\sum }_n{B}_n{t}^n/n!$, the right hand side thus will give the product of the generating function of the constant sequence $a_n=1$ (which we just saw is $\exp (t)$) with $F(t)$. This reflects the split that gave us the recursion – into a set of size $k$ containing the number $1$ (the total number of such sets being $1$ once the numbers are chosen), and a partition of the remaining numbers.

The left hand side is the exponential generating function of $B_{n+1}$ which is just the derivative of $F(t)$, thus we have that

$$\frac{\text{d}}{\text{d}t}F(t)=\sum _{n\ge 1}\frac{B_n{t}^{n-1}}{(n-1)!}=\sum _{n\ge 0}\frac{B_{n+1}{t}^n}{n!}=\exp (t)F(t).$$

This is a separable differential equation, it’s solution is

$$F(t)=c\cdot \exp (\exp (t))$$

for some constant $c$. As $F(0)=1$ we solve for $c=\exp (-1)$ and hence get the exponential generating function

$$\sum _n\frac{B_n{t}^n}{n!}=\exp (\exp (t)-1).$$

There is no nice way to express the power series coefficients of this function in closed form, a Taylor approximation is (with denominators being deliberately kept in the form of $n!$ to allow reading off the Bell numbers):

$$1+t+\frac{2t^2}{2!}+\frac{5t^3}{3!}+\frac{15t^4}{4!}+\frac{52t^5}{5!}+\frac{203t^6}{6!}+\frac{877t^7}{7!}+\frac{4140t^8}{8!}+\frac{21147t^9}{9!}+\frac{115975t^{10}}{10!}.$$

One, somewhat surprising, application of Bell numbers is to consider rhyme schemes. Given a sequence of $n$ lines, the lines which rhyme form the cells of a partition of $\{1,\mathrm{\dots },n\}$. For example, the partition $\{\{1,2,5\},\{3,4\}\}$ is the scheme AABBA used by Limericks, while Poe’s The Raven uses AABCCCBBB or

$$\{\{1,2\},\{3,7,8,9\},\{4,5,6\}\}.$$

We can read off the Taylor expansion that $B_5=52$. The classic 11th century Japanese novel Genji monogatari (The Tale of Genji) has 54 chapters of which first and last are considered “extra”. The remaining 52 chapters are introduced each with a 5 line poem in one of the 52 possible rhyme schemes and a symbol illustrating the scheme. These symbols, see figure 5, the Genji-mon, have been used extensively in Art. See https://www.viewingjapaneseprints.net/texts/topics_faq/genjimon.html

Figure 5: The Genji-mon

ja.wikipedia.org

2 Stirling numbers

We apply the same idea to the Stirling numbers of the second kind, $S(n,k)$ denoting the number of partitions of $n$ into $k$ (non-empty) parts. According to 8, part 3) there are $k!S(n,k)$ order-significant partitions of $n$ into $k$ parts.

We denote the associated exponential generating function (for order-significant partitions) by

$${𝒮}_k(t)=\sum _{n}k!S(n,k)\frac{t^n}{n!}.$$

We also know that there is – apart from the empty set – exactly one partition into one cell. That is

$${𝒮}_1(t)=t+\frac{t^2}{2!}+\frac{t^3}{3!}+\mathrm{\cdots }=\exp (t)-1$$

If we have a partition into $k$-parts, we can fix the first cell and then partition the rest further. Thus, for $k>1$ we have that

$${𝒮}_k(t)={𝒮}_1(t)\cdot {𝒮}_{k-1}(t),$$

which immediately gives that

$${𝒮}_k(t)={(\exp (t)-1)}^k$$

We deduce that the Stirling numbers of the second kind have the exponential generating function

$$\sum _{n}S(n,k)\frac{t^n}{n!}=\frac{{(\exp (t)-1)}^k}{k!}.$$

Using the fact that $B_n={\sum }_{k=1}^{n}S(n,k)$, we thus get the exponential generating function for the Bell numbers as

${\displaystyle \sum _n}{B}_n{\displaystyle \frac{t^n}{n!}}$ $=$ ${\displaystyle \sum _k}{\displaystyle \sum _n}S(n,k){\displaystyle \frac{t^n}{n!}}$

$=$ ${\displaystyle \sum _k}{\displaystyle \frac{{(\exp (t)-1)}^k}{k!}}=\exp (\exp (t)-1)$

in agreement with the above result.

We also can use the exponential generating function for the Stirling numbers to deduce a coefficient formula for them:

Lemma 6.1.

$$S(n,k)=\frac{1}{k!}\sum _{i=1}^k{(-1)}^{k-i}\left(\genfrac{}{}{0pt}{}{k}{i}\right)i^n.$$

Proof 6.2.

We first note that – as $0^n=0$ – the $i$-sum could start at $1$ or $0$ alternatively without changing the result.

Then multiplying through with $k!$, we know by the binomial formula that

$k!{\displaystyle \sum _n}S(n,k){\displaystyle \frac{t^n}{n!}}$ $=$ ${(\exp (t)-1)}^k={\displaystyle \sum _{i=0}^k}\left({\displaystyle \genfrac{}{}{0pt}{}{k}{i}}\right)\exp {(t)}^i{(-1)}^{k-i}$

$=$ ${\displaystyle \sum _{i=0}^k}\left({\displaystyle \genfrac{}{}{0pt}{}{k}{i}}\right)\exp (i\cdot t){(-1)}^{k-i}={\displaystyle \sum _{i=0}^k}\left({\displaystyle \genfrac{}{}{0pt}{}{k}{i}}\right)\left({\displaystyle \sum _n}{\displaystyle \frac{{(it)}^n}{n!}}\right){(-1)}^{k-i}$

$=$ ${\displaystyle \sum _n}\left({\displaystyle \sum _{i=0}^k}\left({\displaystyle \genfrac{}{}{0pt}{}{k}{i}}\right){(-1)}^{k-i}{i}^n\right){\displaystyle \frac{t^n}{n!}}.$

and we read off the coefficients.

3 Involutions

Finally, let us use this in a new situation:

Definition 10.

A permutation $\pi$ on $\{1,\mathrm{\dots },n\}$ is called an involution OEIS A000085 if ${\pi }^2=1$, i.e. ${(i^{\pi })}^{\pi }=i$ for all $i$.

We want to determine the number $s_n$ of involutions on $n$ points.

Consider the number of cycles (including $1$-cycles, that is fixed points). Let $s_r(n)$ be the number of involutions with exactly $r$ cycles. Clearly $s_0(0)=1$, $s_1(0)=0$, $s_1(1)=1$, $s_1(2)=1$, hence the exponential generating function for a single cycle is $S_1(t)=t+\frac{t^2}{2}$.

When considering an arbitrary involution, we can split off a cycle, seemingly leading to a formula

$${\left(t+\frac{t^2}{2}\right)}^r.$$

But (similar as when we considered a generating function for $k!S(n,k)$ for the Stirling numbers), such a product of exponential generating functions will consider the arrangement of cycles, i.e. consider $(1,2)(3,4)$ different from $(3,4)(1,2)$. We correct this by dividing by $r!$ and thus get

$$S_r(t)=\frac{1}{r!}{\left(t+\frac{t^2}{2}\right)}^r$$

and thus for the exponential generating function of the number of involutions a sum over all possible $r$:

$$S(t)=\sum _{r=0}^{\mathrm{\infty }}{S}_r(t)=\sum _r\frac{1}{r!}{\left(t+\frac{t^2}{2}\right)}^r=\exp (t+\frac{t^2}{2})=\exp (t)\exp \left(\frac{t^2}{2}\right).$$

We easily write down a power series for the two factors

$\exp (t)$ $=$ ${\displaystyle \sum _n}{\displaystyle \frac{t^n}{n!}}$

$\exp \left({\displaystyle \frac{t^2}{2}}\right)$ $=$ ${\displaystyle \sum _n}{\displaystyle \frac{t^{2n}}{2^n\cdot n!}}$

and multiply out, yielding

$S(t)$ $=$ $\left({\displaystyle \sum _n}{\displaystyle \frac{t^{2n}}{2^n\cdot n!}}\right)\cdot \left({\displaystyle \sum _n}{\displaystyle \frac{t^n}{n!}}\right)$

$=$ ${\displaystyle \sum _m}{\displaystyle \sum _{k=0}^{\lfloor m/2\rfloor }}{\displaystyle \frac{t^{2k}{t}^{m-2k}}{2^{k}k!(m-2k)!}}$

and thus (again introducing a factor of $n!$ for making up for the exponential generating function)

$$s_n=\sum _{k=0}^{\lfloor m/2\rfloor }\frac{n!}{2^{k}k!(n-2k)!}.$$

Chapter 3 Inclusion, Incidence, and Inversion

It is calculus exam week and, as every time, a number of students were reported to require alternate accommodations:

• $14$ students are sick.

• $12$ students are scheduled to play for the university Quiddich team at the county tournament.

• $12$ students are planning to go on the restaurant excursion for the food appreciation class.

• $5$ students on the Quiddich team are sick (having been hit by balls).

• $4$ students are scheduled for the excursion and the tournament.

• $3$ students of the food appreciation class are sick (with food poisoning), and

• $2$ of these students also planned to go to the tournament, i.e. have all three excuses.

The course coordinator wonders how many alternate exams need to be provided.

Using a Venn diagram and some trial-and-error, it is not hard to come up with the diagram in figure 1, showing that there are $28$ alternate exams to offer.

Figure 1: An example of Inclusion/Exclusion

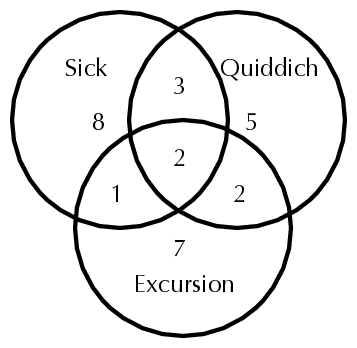
1 The Principle of Inclusion and Exclusion

By the method of exclusion, I had arrived at this result, for no other hypothesis would meet the facts. A Study in Scarlet
Arthur Conan Doyle

The Principle of Inclusion and Exclusion (PIE) formalizes this process for an arbitrary number of sets:

Let $X$ be a set and $\{A_1,\mathrm{\dots },A_n\}$ a family of subsets. For any subset $I\subset \{1,\mathrm{\dots },n\}$ we define

$$A_I=\bigcap _{i\in I}{A}_i,$$

using that $A_{\mathrm{\varnothing }}=X$. Then

Lemma 1.1.

The number of elements that lie in none of the subsets $A_i$ is given by

$$\sum _{I\subset \{1,\mathrm{\dots },n\}}{(-1)}^{\left|I\right|}\left|A_I\right|.$$

Proof 1.2.

Take $x\in X$ and consider the contribution of this element to the given sum. If $x\notin A_i$ for any $i$, it only is counted for $I=\mathrm{\varnothing }$, that is contributes $1$.

Otherwise let $J=\{1\le a\le n\mid x\in A_a\}$ and let $j=\left|J\right|$. We have that $x\in A_I$ if and only if $I\subset J$. Thus $x$ contributes

$$\sum _{I\subset J}{(-1)}^{\left|I\right|}=\sum _{i=0}^j\left(\genfrac{}{}{0pt}{}{j}{i}\right){(-1)}^i={(1-1)}^j=0$$

As a first application we determine the number of derangements on $n$ points in an different way:

Let $X=S_n$ be the set of all permutations of degree $n$, and let $A_i$ be the set of all permutations $\pi$ with $i^{\pi }=i$. Then $S_n\setminus {\bigcup }_i{A}_i$ is exactly the set of derangements, there are $\left(\genfrac{}{}{0pt}{}{n}{i}\right)$ possibilities to intersect $i$ of the $A_i$’s, and the formula gives us:

$$d(n)=\sum _{i=0}^n{(-1)}^i\left(\genfrac{}{}{0pt}{}{n}{i}\right)(n-i)!=n!\sum _{i=0}^n\frac{{(-1)}^i}{i!}.$$

For a second example, we calculate the number of surjective mappings from an $n$-set to a $k$-set (which we know already from 8 to be $k!S(n,k)$):

Let $X$ be the set of all mappings from $\{1,\mathrm{\dots },n\}$ to $\{1,\mathrm{\dots },k\}$, then $\left|X\right|=k^n$. Let $A_i$ be the set of those mappings $f$, such that $i$ is not in the image of $f$, so $\left|A_i\right|={(k-1)}^n$. More generally, if $I\subset \{1,\mathrm{\dots }k\}$ we have that $\left|A_I\right|={(k-\left|I\right|)}^n$. The surjective mappings are exactly those in $X$ outside any of the $A_i$, thus the formula gives us the count

$$\sum _{i=0}^k{(-1)}^i\left(\genfrac{}{}{0pt}{}{k}{i}\right){(k-i)}^n,$$

using again that there are $\left(\genfrac{}{}{0pt}{}{k}{i}\right)$ possible sets $I$ of cardinality $i$.

The factor ${(-1)}^i$ in a formula often is a good indication that inclusion/exclusion is to be used.

Lemma 1.3.

Proof 1.4.

To use PIE, the sets $A_i$ need to involve choosing from an $n$, set, and after choosing $i$ of these we must choose from a set of size $m+n-i$.

Consider a bucket filled with $n$ blue balls, labeled with $1,\mathrm{\dots },n$, and $m$ red balls. How many selections of $k$ balls only involve red balls? Clearly the answer is the right hand side of the formula.

Let $X$ be the set of all $k$-subsets of balls and $A_i$ those subsets that contain blue ball number $i$, then PIE gives the left side of the formula.

We finish this section with an application from number theory. The Euler function $\phi (n)$ counts the number of integers $1\le k\le n$ with $\gcd (k,n)=1$.

Suppose that $n={\prod }_{i=1}^r{p}_i^{e_i}$, $X=\{1,\mathrm{\dots },n\}$ and $A_i$ the integers in $X$ that are multiples of $p_i^{e_i}$. Thus $|A_i|=\frac{n}{p_i^{e_i}}$ and for $I=\{i_1,\mathrm{\dots },i_k\}$ we have that $A_I$ consists of multiples of $P_I=p_{i_1}\mathrm{\cdots }{p}_{i_k}$ and thus $|A_i|=\frac{n}{P_I}$. Then $\phi (n)$ counts the number of elements in $X$ that do not lie in any of the $A_i$ and (inclusion/exclusion)

$$\phi (n)=n-\sum _{i=1}^r\frac{n}{p_i}+\sum _{1\le i,j\le r}\frac{n}{p_i{p}_j}-\mathrm{\cdots }=n\prod \left(1-\frac{1}{p_i}\right).$$

with the second identity obtained by multiplying out the product on the right hand side.

We also note – exercise LABEL:phisum – that ${\sum }_{d|n}\phi (d)=n$. On its own this looks as if it is entirely separate from the inclusion/exclusion concept we just considered. But by generalize the concept of a hierarchy, given hitherto through inclusion of subsets, to more general situations, we shall see that this is a structural consequence of the previous formula.

2 Partially Ordered Sets and Lattices

The doors are open; and the surfeited grooms
Do mock their charge with snores:
I have drugg’d their possets,
That death and nature do contend about them
Macbeth, Act II, Scene II
William Shakespeare

A poset or partially ordered set is a set $A$ with a relation $R\subset A\times A$ on the elements of $A$ which we will typically write as $a\le b$ instead of $(a,b)\in R$, such that for all $a,b,c\in A$:

(reflexive)

$a\le a$.

(antisymmetric)

$a\le b$ and $b\le a$ imply that $a=b$.

(transitive)

$a\le b$ and $b\le c$ imply that $a\le c$.

The elements of a poset thus are the elements of $A$, not those of the underlying relation and is cardinality is that of $A$.

For example, $A$ could be the set of subsets of a particular set, and $\le$ with be the “subset or equal” relation.

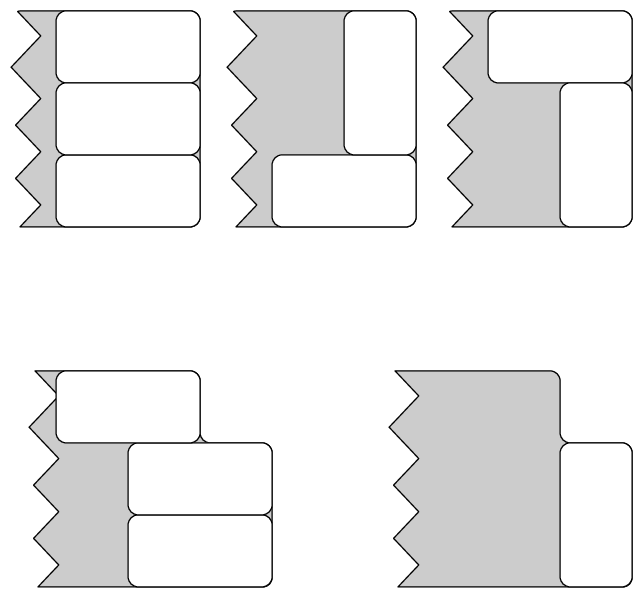
A convenient way do describe a poset for a finite set $A$ is by its Hasse-diagram. Say that $a$ covers $b$ if $a\ge b$, $a\ne b$ and there is no $a\ne c=\ne b$ with $a\ge c\ge b$. The Hasse diagram of the poset is a graph in the plane which connects two vertices $a$ and $b$ only if $a$ covers $b$, and in this case the edge from $b$ to $a$ goes upwards.

Because of transitivity, we have that $a\le b$ if and only if one can go up along edges from $a$ to reach $b$.

Figure 2: Hasse Diagrams of Small Posets and Lattices

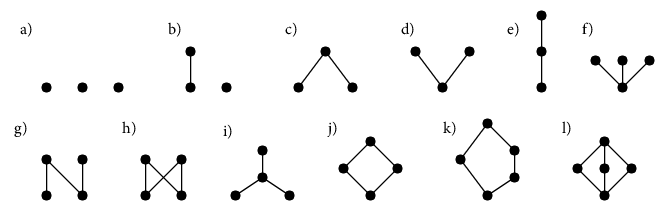
Figure 2 gives a number of examples of posets, given by their Hasse diagrams, including all posets on 3 elements.

An isomorphism of posets is a bijection that preserves the $\le$ relation.

An element in a poset is called maximal if there is no larger (wrt. $\le$) element, minimal is defined in the same way. Posets might have multiple maximal and minimal elements.

For another cute example  consider in Figure 3, left, the arrangement of fruits according to convenience and taste, as given by https://xkcd.com/388/.

Figure 3: Fruits, arranged by subjective taste and ease-of-use

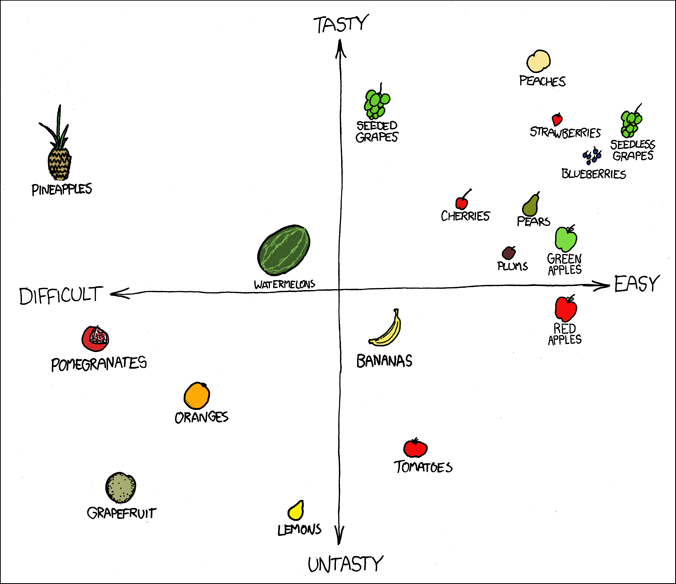
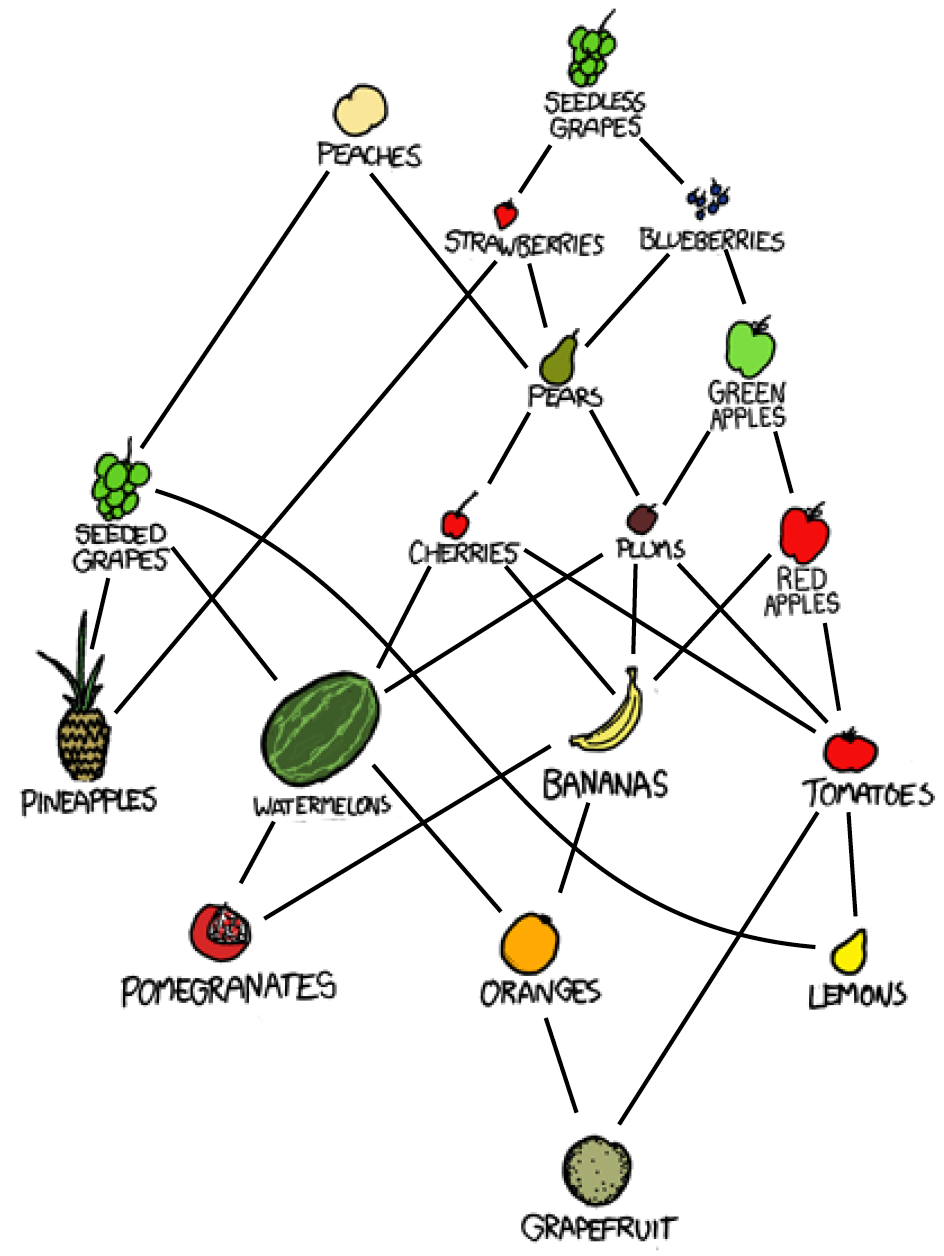
R. Munroe, F*** Grapefruit, https://xkcd.com/388/, and [axue], p.108

We can read of a partial order from this by declaring a fruit as “better” than another, if it both more tasty and easier to consume. The resulting Hasse diagram is on the right side of Figure 3. It is easily seen that not every pair of fruits is comparable this way, and that there is no universal “best” or “worst” fruit.

1 Linear extension

My scheme of Order gave me the most trouble Autobiography
Benjamin Franklin

A partial order is called a total order, if for every pair $a,b\in A$ of elements we have that $a\le b$ or $b\le a$.

While this is not part of our definition, we can always embed a partial order into a total order.

Proposition 11.

Let $R\subset A\times A$ be a partial order on $A$. Then there exists a total order (called a linear extension) $T\subset A\times A$ such that $R\subset T$.

To avoid set acrobatics we shall prove this only in the case of a finite set $A$. Note that in Computer science the process of finding such an embedding is called a topological sorting.

Proof 2.1.

We proceed by induction over the number of pairs $a,b$ that are incomparable. In the base case we already have a total order.

Otherwise, let $a,b$ such an incomparable pair. We set (arbitrarily) that . Now let

$$L=\{x\in A\mid x{\le }_{R}a\},U=\{x\in A\mid b{\le }_{R}x\}$$

We claim that $S=R\cup \{(l,u)\mid l\in L,u\in u\}$ is a partial order. As $(a,b)\in S$ it has fewer incomparable pairs, this shows by induction that there exists a total order $T\supset S\supset R$, proving the theorem.

Since $R$ is reflexive, $S$ is. For antisymmetry, suppose by contradiction that for some $x\ne y$ we have that $(x,y),(y,x)\in S$. Since $R$ is a partial order, not both could have been in $R$.

Thus assume (WLOG) that

$$(y,x)\in S\setminus R\subset \{(l,u)\mid l\in L,u\in u\}.$$

This implies that $y{\le }_{R}a$ and $b{\le }_{R}x$. If $(x,y)\in R$, this implies by transitivity that $b{\le }_{R}a$, contradicting the choice of $a,b$. If $(x,y)\notin R$, then also $(x,y)\in S\setminus R$ and thus by definition $x{\le }_{R}a$. Transitivity implies again $b{\le }_{R}x{\le }_{R}a$ in contradiction to the choice of $a,b$.

For transitivity, the definition of $S$ implies that we cannot have transitivity for pairs in $S\setminus R$. Thus first suppose that $(x,y)\in S\setminus R$ and $(y,z)\in S$. Then $(y,z)\in R$, as otherwise $b{\le }_{R}y{\le }_{R}a$. But then $b{\le }_{R}y{\le }_{R}z$, implying that $(x,z)\in S$. The other remaining case is analog.

This theorem implies that we can always label the elements of a countable poset with positive integers, such that the poset ordering implies the integer ordering. Such an embedding is in general not unique, see Theorem 21.

The case of a totally ordered subset gets a special name:

Definition 12.

A chain in a poset $P$ is a subset of $P$ such that any two elements of it are comparable. (That is, restricted to the chain the order is total.)

2 Lattices

Definition 13.

Let $A$ be a poset and $a,b\in A$.

• A greatest lower bound of $a$ and $b$ is an element $c\le a,b$ which is maximal in the set of elements with this property.

• A least upper bound of $a$ and $b$ is an element $c\ge a,b$ which is minimal in the set of elements with this property.

$A$ is a lattice if any pair $a,b\in A$ have a unique greatest lower bound, called the meet and denoted by $a\wedge b$; as well as unique least upper bound, called the join and denoted by $a\vee b$.

Amongst the Hasse diagrams in figure 2, e,j,k,l) are lattices, while the others are not. Lattices always have unique maximal and minimal elements, sometimes denoted by $0$ (minimal) and $1$ (maximal).

Other examples of lattices are:

1. Given a set $X$, let $A=𝒫(X)=\{Y\subseteq X\}$ the power set of $X$ with $\le$ defined by inclusion. Meet is the intersection, join the union of subsets.

2. Given an integer $n$, let $A$ be the set of divisors of $n$ with $\le$ given by “divides”. Meet and join are $\gcd$, respectively lcm.

3. For an algebraic structure $S$, let $A$ be the set of all substructures (e.g. group and subgroups) of $S$ and $\le$ given by inclusion. Meet is the intersection, join the substructure spanned by the two constituents.

4. For particular algebraic structures there might be classes of substructures that are closed under meet and join, e.g. normal subgroups. These then form a (sub)lattice.

Using meet and join as binary operations, we can axiomatize the structure of a lattice:

Proposition 14.

Let $X$ be a set with two binary operations $\wedge$ and $\vee$ and two distinguished elements $0,1\in X$. Then $(X,\wedge ,\vee ,0,1)$ is a lattice if and only if the following axioms are satisfies for all $x,y,z\in X$:

Associativity:

$x\wedge (y\wedge z)=(x\wedge y)\wedge z$ and $x\vee (y\vee z)=(x\vee y)\vee z$;

Commutativity:

$x\wedge y=y\wedge x$ and $x\vee y=y\vee x$;

Idempotence:

$x\wedge x=x$ and $x\vee x=x$;

Inclusion:

$(x\vee y)\wedge x=x=(x\wedge y)\vee x$;

Maximality:

$x\wedge 0=0$ and $x\vee 1=1$.

Proof 2.2.

The verification that these axioms hold for a lattice is left as exercise to the reader.

Vice versa, assume that these axioms hold. We need to produce a poset structure and thus define that $x\le y$ iff $x\wedge y=x$. Using commutativity and inclusion this implies the dual property that $x\vee y=(x\wedge y)\vee y=y$.

To show that $\le$ is a partial order, idempotence shows reflexivity. If $x\le y$ and $y\le x$ then $x=x\wedge y=y\wedge x=y$ and thus antisymmetry. Finally suppose that $x\le y$ and $y\le z$, that is $x=x\wedge y$ and $y=y\wedge z$. Then

$$x\wedge z=(x\wedge y)\wedge z=x\wedge (y\wedge z)=x\wedge y=x$$

and thus $x\le z$. Associativity gives us that $x\wedge y\le x,y$ if also $z\le x,y$ then

$$z\wedge (x\wedge y)=(z\wedge x)\wedge y=z\wedge y=z$$

and thus $z\le x\wedge y$, thus $x\wedge y$ is the unique greatest lower bound. The least upper bound is proven in the same way and the last axiom shows that $0$ is the unique minimal and $1$ the unique maximal element.

Definition 15.

An element $x$ of a lattice $L$ is join-irreducible (JI) if $x\ne 0$ and if $x=y\vee z$ implies that $x=y$ or $x=z$.

For example, figure 4 shows a lattice in which the black vertices are JI, the others not.

If we take the lattice of subsets of a set, the join-irreducibles are the 1-element sets. If we take divisors of $n$, the join-irreducibles are prime powers.

When representing elements of a finite lattices, it is possible to do so by storing the JI elements once and representing every element based on the JI elements that are below. This is used for example in one of the algorithms for calculating the subgroups of a group.

3 Product of posets

The cartesian product provides a way to construct new posets (or lattices) from old ones: Suppose that $X,Y$ are posets with orderings ${\le }_X$, ${\le }_Y$, we define a partial order on $X\times Y$ by setting

$$(x_1,y_1)\le (x_2,y_2)\text{if and only if}{x}_1{\le }_X{x}_2\text{and}{y}_1{\le }_Y\le y_2.$$

Proposition 16.

This is a partial ordering, so $X\times Y$ is a poset. If furthermore both $X$ and $Y$ are lattices, then so is $X\times Y$.

The proof of this is exercise LABEL:posetproduct.

This allows us to describe two familiar lattices as constructed from smaller pieces (with a proof also delegated to the exercises):

Proposition 17.

a) Let $\left|A\right|=n$ and $𝒫(A)$ the power-set lattice (that is the subsets of $A$, sorted by inclusion). Then $𝒫(A)$ is (isomorphic to) the direct product of $n$ copies of the two element lattice $\{0,1\}$.
b) For an integer $n={\prod }_{i=1}^r{p}_i^{e_i}>1$ written as a product of powers of distinct primes, let $𝒟(n)$ be the lattice of divisors of $n$. Then $𝒟(n)\cong 𝒟(p_1^{e_1})\times \mathrm{\cdots }\times 𝒟(p_r^{e_r})$.

3 Distributive Lattices

A lattice $L$ is distributive, if for any $x,y,z\in L$ one (and thus also the other) of the two following laws hold:

$x\vee (y\wedge z)$ $=$ $(x\vee y)\wedge (x\vee z)$

$x\wedge (y\vee z)$ $=$ $(x\wedge y)\vee (x\wedge z)$

These laws clearly hold for the lattice of subsets of a set or the lattice of divisors of an integer $n$.

Lattices of substructures of algebraic structures are typically not distributive, the easiest example (diagram l) in figure 2) is the lattice of subgroups of $C_2\times C_2$ which also is the lattice of subspaces of $F_2^2$.

If $P=(X,\le )$ is a poset, a subset $Y\le X$ is an order ideal, if for any $y\in Y$ and $z\in X$ we have that $z\le y$ implies $z\in Y$.

Lemma 3.1.

The set of order ideals is closed under union and intersection.

Proof 3.2.

Let $A,B$ be order ideals and $y\in A\cup B$ and $z\le y$. Then $y\in A$ or $y\in B$. In the first case we have that $z\in A$, in the second case that $z\in B$, and thus always $z\in A\cup B$. The same argument also works for intersections.

This implies:

Lemma 3.3.

The set of order ideals of $P$, denoted by $J(P)$ is a lattice under intersection and union.

As a sublattice of the lattice of subsets, $J(P)$ is clearly distributive.

For example, if $P$ is the poset on 4 elements with a Hasse diagram given by the letter $N$ (figure 2, g) then figure 4 describes the lattice $J(P)$.

Figure 4: Order-ideal lattice for the “N” poset.

In fact, any finite distributive lattice can be obtained this way

Theorem 18 (Fundamental Theorem for Finite Distributive Lattices, Birkhoff).

Let $L$ be a finite distributive lattice. Then there is a unique (up to isomorphism) finite poset $P$, such that $L\cong J(P)$.

To prove this theorem we use the following definition:

Definition 19.

For any element $x$ of the poset $P$, let $\downarrow x=\{y\mid y\le x\}$ be the principal order ideal generated by $x$.

Lemma 3.4.

An order ideal of a finite poset $P$ is join irreducible in $J(P)$ if and only it is principal.

Proof 3.5.

First consider a principal order ideal $\downarrow x$ and suppose that $\downarrow x=b\vee c$ with $b$ and $c$ being order ideals. Then $x\in b$ or $x\in c$, which by the order ideal property implies that $\downarrow x\subset b$ or $\le x\subset c$.

Vice versa, suppose that $a$ is a join irreducible order ideal and assume that $a$ is not principal. Then for any $x\in a$, $\downarrow x$ is a proper subset of $a$. But clearly $a={\bigcup }_{x\in a}\downarrow x$.

Corollary 20.

Given a finite poset $P$, the set of join-irreducibles of $J(P)$, considered as a subposet of $J(P)$, is isomorphic to $P$.

Proof 3.6.

Consider the map that maps $x$ to $\downarrow x$. It maps $P$ bijective to the set of join-irreducibles, and clearly preserves inclusion.

We now can prove theorem 18

Proof 3.7.

Given a distributive lattice $L$, let $X$ be the set of join-irreducible elements of $L$ and $P$ be the subposet of $L$ formed by them. By corollary 20, this is the only option for $P$ up to isomorphism, which will show uniqueness.

Let $\varphi :L\to J(P)$ be defined by $\varphi (a)=\{x\in X\mid x\le a\}$, that is it assigns to every element of $L$ the JI elements below it. (Note that indeed $\varphi (a)$ is an order ideal.). We want to show that $\varphi$ is an isomorphism of lattices.

Step1: Clearly we have that $a={\bigvee }_{x\in \varphi (a)}x$ for any $a\in L$ (using the join over the empty set equal to $0$). Thus $\varphi$ is injective.

Step 2: To show that $\varphi$ is surjective, let $Y\in J(P)$ be an order ideal of $P$, and let $a={\bigvee }_{y\in Y}y$. We aim to show that $\varphi (a)=Y$: Clearly every $y\in Y$ also has $y\le a$, so $Y\subset \varphi (a)$. Next take a join irreducible $x\in \varphi (a)$, that is $x\le a$. Then $x\le {\bigvee }_{y\in Y}y$ and thus

$$x=x\wedge \left(\underset{y\in Y}{\bigvee }y\right)=\underset{y\in Y}{\bigvee }(x\wedge y)$$

by the distributive law. Because $x$ is JI, we must have that $x=x\wedge y$ for some $y\in Y$, implying that $x\le y$. But as $Y$ is an order ideal this implies that $x\in Y$. Thus $\varphi (a)\subset Y$ and thus equality, showing that $\varphi$ is surjective.

Step 3: We finally need to show that $\varphi$ maps the lattice operations: Let $x\in X$. Then $x\le a\wedge b$ if and only if $x\le a$ and $x\le b$. Thus $\varphi (a\wedge b)=\varphi (a)\cap \varphi (b)$.

For the join, take $x\in \varphi (a)\cup \varphi (b)$. Then $x\in \varphi (a)$, implying $x\le a$, or (same argument) $x\le b$; therefore $x\le a\vee b$. Vice versa, suppose that $x\in \varphi (a\vee b)$, so $x\le a\vee b$ and thus

$$x=x\wedge (a\vee b)=(x\wedge a)\vee (x\wedge b).$$

Because $x$ is JI that implies $x=x\wedge a$, respectively $x=x\wedge b$.

In the first case this gives $x\le a$ and thus $x\in \varphi (a)$; the second case similarly gives $x\in \varphi (b)$.

We close with a further use of the order ideal lattice:

Theorem 21.

Let $P$ be a poset of size $m$. The number of different linear orderings of $P$ is equal to the number of different chains of (maximal) length $m$ in $J(P)$.

Proof 3.8.

Exercise.

4 Chains, Antichains, and Extremal Set Theory

Man is born free;
and everywhere he is in chains
The Social Contract
Jean-Jacques Rousseau

We start with a definition dual to that of a chain:

Definition 22.

An antichain in a poset is a subset, such that any two (different) elements are incomparable.

We shall consider partitions of (the elements of) a poset into a collection of chains (or of antichains).

Clearly a chain $C$ and antichain $A$ can intersect in at most one element. This gives the following duality:

Lemma 4.1.

Let $P$ be a poset.
a) If $P$ has a chain of size $r$, then it cannot be partitioned in fewer than $r$ antichains.
b) If $P$ has an antichain of size $r$, then it cannot be partitioned in fewer than $r$ chains.

A stronger version of this goes usually under the name of Dilworth’s theorem.

Theorem 23 (Dilworth, 1950).

The minimum number $m$ of chains in a partition of a finite poset $P$ is equal to the maximum number $M$ of elements in an antichain.

Proof 4.2.

The previous lemma shows that $m\ge M$, so we only need to show that we can partition $P$ into $M$ chains. We use induction on $\left|P\right|$, in the base case $\left|P\right|=1$ nothing needs to be shown.

Consider a chain $C$ in $P$ of maximal size. If every antichain in $P\setminus C$ contains at most $M-1$ elements, we apply induction and partition $P\setminus C$ into $M-1$ chains and are done.

Thus assume now that $\{a_1,\mathrm{\dots },a_M\}$ was an antichain in $P\setminus C$. Let

$S^{-}$ $=$ $\{x\in P\mid x\le a_i\text{ for some }i\}$

$S^{+}$ $=$ $\{x\in P\mid x\ge a_i\text{ for some }i\}$

Then $S^{-}\cup S^{+}=P$, as there otherwise would be an element we could add to the antichain and increase its size.

As $C$ is of maximal size, the largest element of $C$ cannot be in $S^{-}$, and thus we can apply induction to $S^{-}$. As there is an antichain of cardinality $M$ in $S^{-}$, we partition $S^{-}$ into $M$ disjoint chains.

Similarly we partition $S^{+}$ into $M$ disjoint chains. But each $a_i$ is maximal element of exactly one chain in $S^{-}$ and minimal element of exactly one chain of $S^{+}$. We can combine these chains at the $a_i$’s and thus partition $P$ into $M$ chains.

Corollary 24.

If $P$ is a poset with $nm+1$ elements, it has a chain of size $n+1$ or an antichain of size $m+1$.

Proof 4.3.

Suppose not, then every antichain has at most $m$ elements and by Dilworth’s theorem we can partition $P$ into $m$ chains of size $\le n$ each, so $\left|P\right|\le mn$.

Corollary 25 (Erdős-Szekeres, 1935).

Every sequence of $nm+1$ distinct integers contains an increasing subsequence of length at least $n+1$, or a decreasing subsequence of at length least $m+1$.

Proof 4.4.

Suppose the sequence is $a_1,\mathrm{\dots },a_N$ with $N=nm+1$. We construct a poset on $N$ elements $x_1,\mathrm{\dots },x_N$ by defining $x_i\le x_j$ if and only if $i\le j$ and $a_i\le a_j$. (Verify that it is a partial order!)

The theorems of this section in fact belong into a bigger context that has its own chapter, chapter 4, devoted to.

A similar argument applies in the following two famous theorems, that are part of foundational material of extremal set theory.

Theorem 26 (Sperner, 1928).

Let $N=\{1,\mathrm{\dots },n\}$ and $A_1,\mathrm{\dots }{A}_m\subset N$, such that $A_i\not\subset A_j$ if $i\ne j$. Then $m\le \left(\genfrac{}{}{0pt}{}{n}{\lfloor n/2\rfloor }\right)$.

Proof 4.5.

Consider the poset of subsets of $N$ and let $𝒜=\{A_1,\mathrm{\dots },A_m\}$. Then $𝒜$ is an antichain.

A maximal chain $𝒞$ in this poset will consist of sets that iteratively add one new point, so there are $n!$ maximal chains, and $k!(n-k)!$ maximal chains that involve a particular $k$-subset of $N$.

We now count the pairs $(A,𝒞)$ such that $A\in 𝒜$ and $𝒞$ is a maximal chain with $A\in 𝒞$. As a chain can contain at most one element of an antichain this is at most $n!$.

On the other hand, denoting by $a_k$ the number of sets $A_i$ with $\left|A_i\right|=k$, we know there are

$$n!\ge \sum _{k=0}^{n}k!(n-k)!a_k=n!\left(\sum _{k=0}^n\frac{a_k}{\left(\genfrac{}{}{0pt}{}{n}{k}\right)}\right)$$

such pairs. As $\left(\genfrac{}{}{0pt}{}{n}{k}\right)$ is maximal for $k=\lfloor n/2\rfloor$ we get

$$\left(\genfrac{}{}{0pt}{}{n}{\lfloor n/2\rfloor }\right)\ge \left(\genfrac{}{}{0pt}{}{n}{\lfloor n/2\rfloor }\right)\sum _{k=0}^n\frac{a_k}{\left(\genfrac{}{}{0pt}{}{n}{k}\right)}\ge \sum _{k=0}^n{a}_k=m.$$

We note that equality is achieved if $𝒜$ is the set of all $\lfloor n/2\rfloor$-subsets of $N$.

Theorem 27 (Erdős-Ko-Rado, 1961).

Let $𝒜=\{A_1,\mathrm{\dots },A_m\}$ a collection of $m$ distinct $k$-subsets of $N=\{1,\mathrm{\dots },n\}$, where $k\le n/2$, such that any two subsets have nonempty intersection. Then $m\le \left(\genfrac{}{}{0pt}{}{n-1}{k-1}\right)$.

Proof 4.6.

Consider “cyclic $k$-sequences” $ℱ=\{F_1,\mathrm{\dots },F_n\}$ with $F_i=\{i,i+1,\mathrm{\dots },i+k-1\}$, taken “modulo $n$” (that is each number should be $((x-1)modn)+1$).

Note that $\left|𝒜\cap ℱ\right|\le k$, since if some $F_i$ equals $A_j$, then any only other $F_l\in 𝒜$ must intersect $F_i$, so we only need to consider (again considering indices modulo $n$) $F_l$ for $i-k+1\le l\le i+k-1$. But $F_l$ will not intersect $F_{l+k}$, allowing at most for a set of $k$ subsequent $F_i$’s to be in $𝒜$.

As this holds for an arbitrary $𝒜$, the result remains true after applying any arbitrary permutation $\pi$ to the numbers in $ℱ$. Thus

$$z:=\sum _{\pi \in S_n}\left|𝒜\cap {ℱ}^{\pi }\right|\le k\cdot n!$$

We now calculate the sum $z$ by fixing $A_j\in 𝒜$, $F_i\in ℱ$ and observe that there are $k!(n-k)!$ permutations $\pi$ such that $F_i^{\pi }=A_j$. Thus $z=m\cdot n\cdot k!(n-k)!$, proving the theorem.

5 Incidence Algebras and Möbius Functions

A common tool in mathematics is to consider instead of a set $S$ the set of functions defined on $S$. To use this paradigm for (finite) posets, define an interval on a poset $P$ for a given pair $x\le y\in P$ as the set $\{z\in P\mid x\le z\le y\}$, and denote by $\text{Int}(P)$ the set of all intervals. (It might be convenient to set $[x,y]=\mathrm{\varnothing }$ if $x]̸ley$.

For a field $K$, we shall consider the set of functions on the intervals:

$$I(P)=I(P,K)=\{f:\text{Int(P)}\to K\}$$

(with $f(\mathrm{\varnothing })=0$) and call it the incidence algebra of $P$. If we denote intervals by their end points $x,y$, we shall write $f(x,y)$ for $f([x,y])$ if $f\in I(P)$.

This set of functions is obviously a $K$-vector space under pointwise operations. We also define a multiplication on $I(P)$ by defining, for $f,g\in I(P)$ a function $fg$ by

$$(fg)(x,y)=\sum _{x\le z\le y}f(x,z)g(z,y)$$

In exercise LABEL:incidencealgebra we will show that with this definition $I(P)$ becomes an associative $K$-algebra with a one, given by

We could consider $I(P)$ as the set of formal $K$-linear combinations of intervals $[x,y]$ and a product defined by

and extended bilinearily.

If $P$ is finite, we can, by theorem 11, arrange the elements of $P$ as $x_1,\mathrm{\dots },x_n$ where $x_i\le x_j$ implies that $i\le j$. Then $I(P)$ is, by exercise LABEL:incalgmatalg isomorphic to the algebra of upper triangular matrices $M=(m_{i,j})$ where $m_{i,j}=0$ if $x_i\nleqq x_j$.

Lemma 5.1.

Let $f\in I(P)$. Then $f$ has a (two-sided) inverse if and only if $f(x,x)\ne 0$ for all $x\in P$.

Proof 5.2.

The property $fg=\delta$ is equivalent to:

$$f(x,x)g(x,x)=1\text{for all }x\in P\text{,}$$

(implying the necessity of $f(x,x)\ne 0$) and

If $f(x,x)\ne 0$ the second formula will define the values $f^{-1}$ uniquely, depending only on the interval $[x,y]$. Reverting the roles of $f$ and $g$ shows the existence of a left inverse and standard algebra shows that both have to be equal.

The zeta function of $P$ is the characteristic function of the underlying relation, that is $\zeta (x,y)=1$ if and only if $x\le y$ (and $\zeta (\mathrm{\varnothing })=0$).

This implies that

$${\zeta }^2(x,y)=\sum _{x\le z\le y}\zeta (x,z)\zeta (z,y)=\sum _{x\le z\le y}1=\left|\{x\mid z\le z\le y\}\right|$$

is the size of the interval.

By Lemma 5.1, $\zeta$ is invertible. The inverse $\mu ={\zeta }^{-1}$ is called the Möbius function of the lattice $P$. The identities

$\mu (x,x)$ $=$ $1$ (1)

$\mu (x,y)$ $=$ (2)

follow from $\mu \zeta =\delta$ and allow for a recursive computation of values of $\mu$ and imply that $\mu$ is integer-valued.

For illustration, we shall compute the Möbius function for a number of common posets.

Lemma 5.3.

Let $P$ be the total order on the numbers $\{1,\mathrm{\dots },n\}$. Then for any $x,y\in P$ we have:

Proof 5.4.

The case of $x=y$ is trivial. If $x+1=y$, the sum in 2 has only one summand, and the result follows. Thus assume that $x\le y$ but $y\notin \{x,x+1\}$. Then

and the result follows by induction on $y-x$.

Lemma 5.5.

If $P$, $Q$ are posets, the Möbius function on $P\times Q$ satisfies

$$\mu ((x_1,y_1),(x_2,y_2))={\mu }_P(x_1,x_2){\mu }_Q(y_1,y_2)$$

Proof 5.6.

It is sufficient to verify that the right hand side of the equation satisfies 2.

Together with Theorem 17 and Lemma 5.3 we get

Corollary 28.

a) For $X,Y\in 𝒫(A)$, we have that $\mu (X,Y)=-1^{\left|Y\right|-\left|X\right|}$ if $X\subseteq Y$, and 0 otherwise.
b) If $x,y$ are divisors of $n$, then in $𝒟(n)$ we have that $\mu (x,y)={(-1)}^d$ if $y/x$ is the product of $d$ different primes, and 0 otherwise.

Part b) explains the name: $\mu (1,n)$ is the value of the classical number theoretic Möbius function.

Part a) connects us back to section 1: The Möbius function gives the coefficients for inclusion/exclusion over an arbitrary poset. We will investigate and clarify this further in the rest of this section.

1 Möbius inversion

The property of being inverse of the incidence function can be used to invert summation formulas with the aid of the Möbius function:

Theorem 29 (Möbius inversion formula).

Let $P$ be a finite poset, and $f,g:P\to K$, where $K$ is a field. Then

$$g(t)=\sum _{s\le t}f(s)\text{for all }t\in P$$

is equivalent to

$$f(t)=\sum _{s\le t}g(s)\mu (s,t)\text{for all }t\in P\text{.}$$

Proof 5.7.

Let $K^P$ be the $K$-vector space of functions $P\to K$. The incidence algebra $I(P)$ acts linearly on this vector space by

$$(f\xi )(t)=\sum _{s\le t}f(s)\xi (s,t).$$

The two equations thus become

$$g=f\zeta ,\text{respectively}f=g\mu ,$$

and their equivalence follows from the fact that $\mu$ is the inverse of $\zeta$.

The classical Möbius inversion formula from Number Theory follows as a special case of this.

If we consider the linear poset $\{1,\mathrm{\dots },n\}$ with total ordering, Lemma 5.3 gives us that (we assume $f(0)=g(0)$) the (unsurprisingly) result that

$$g(k)=\sum _{i=0}^{k}f(i)$$

is equivalent to

$$f(k)=g(k)-g(k-1),$$

the finite difference analog of the fundamental theorem of Calculus!

Going back to the start of the chapter, consider $n$ subsets $A_i$ of a set $X$. We take the the poset $𝒫(X)$ and define, for $I\subset \{1,\mathrm{\dots },n\}$

$f(I)$ $=$ $-1^{\left|I\right|}\left|X\setminus {\displaystyle \bigcup _{i\in I}}{A}_i\right|$

$g(I)$ $=$ $\left|{\displaystyle \bigcap _{i\in I}}{A}_i\right|.$

Then $g(I)={\sum }_{J\subset I}f(J)$ by Inclusion/Exclusion over the complements $X\setminus A_i$, while

$$f(I)=\sum _{J\subset I}g(J)\mu (J,I)=\sum _J-1^{\left|I\right|-\left|J\right|}\left|\bigcap _{j\in J}{A}_j\right|=-1^{\left|I\right|}\left|X\setminus \bigcup A_i\right|$$

is the ordinary inclusion/exclusion formula.

Chapter 4 Connections

Mathematicians are like Frenchmen.
When you talk to them, they translate
it into their own language,
and then it is something quite different.

Die Mathematiker sind eine Art Franzosen;

redet man zu ihnen, so übersetzen sie es

in ihre Sprache, und dann ist es

alsobald ganz etwas anders. Maximen und Reflexionen:

Über Natur und Naturwissenschaft

Johann Wolfgang von Goethe

With so many joints and connections, leaks were plentiful. As the magazine The Builder remarked, in 1856: “The fate of a theater is to be burned. It seems simply a question of time.” Connections
James Burke

In this chapter we will look at connections – both in an applied sense of modeling situations of connected objects, in the abstract sense of connecting mathematical theorems that initially seem to be unrelated, and in connecting concepts that might seem to be hopelessly abstract to practical applications. One of the joys of mathematics is to discover such connections and see the unity of the discipline.

This practical relevance of the results places much of this chapter also in close contact to the realm of (discrete) optimization.

We shall investigate a gaggle of theorems (which each in their area are fundamental), but which turn out to be equivalent in the sense that we can deduce each theorem as a consequence from any other. Furthermore this kind of derivation is often easier than to derive the theorem from scratch. The description owes much to [reichmeider]

Many theorems in this chapter are formulated in the language of graphs: We typically denote a graph by $\mathrm{\Gamma }=(V,E)$ with vertices $V$ and edges $E$ being 2-element sets of vertices. A digraph is a graph with directed edges (that is we consider edges as elements of $V\times V$ instead of $2$-element subsets of $V$). In a digraph, we would allow distinct edges $(x,y)$ and $(y,x)$. Weighted edges means we have a weight function $w:E\to ℝ$.

Our start will be Dilworth’s Theorem 23 that we have proven already:

The minimum number $m$ of chains in a partition of a finite poset $P$ is equal to the maximum number $M$ of elements in an antichain.

1 Halls’ Marriage Theorem

He was, methinks, an understanding fellow who said, ’twas a happy marriage betwixt a blind wife and a deaf husband.

Celuy là s’y entendoit, ce me semble, qui dict qu’un bon mariage se dressoit d’une femme aveugle avec un mary sourd. Essais, Livre III

Michel de Montaigne

Consider a family of subsets $A_1,\mathrm{\dots },A_n\subseteq X$. A system of distinct representatives (SDR) for these sets is an $n$-tuple of distinct elements $x_1,\mathrm{\dots },x_n$ such that $x_i\in A_i$.

SDRs do not have to exist, for example consider $A_1=A_2=\{1\}$.

We define, for a subset $J\subseteq \{1,\mathrm{\dots },n\}$ of indices, a set

$$A(J)=\bigcup _{j\in J}{A}_j.$$

We immediately see a reason for the above example failing: For an SDR to exist, by necessity $\left|A(J)\right|\ge \left|J\right|$ for any such subset $J$, since there are otherwise not sufficiently many elements available to pick distinct representatives. The following Theorem shows this condition is not only necessary, but also sufficient.

Theorem 30 (Halls’ Marriage Theorem).

The family $\{A_1,\mathrm{\dots },A_n\}$ of finite sets has a system of distinct representatives if and only if

$$\left|A(J)\right|\ge \left|J\right|\text{for all}J\subseteq \{1,\mathrm{\dots },n\}.$$ (1)

The name “Marriage Theorem” comes from the following interpretation: Suppose we have a set of $m$ men and $n$ women. We let $A_i$ be the set of men that women $i$ would consider for a potential marriage. Then every women can marry a suitable man if and only if every group of $k$ women together considers at least $k$ men as suitable.

Proof 1.1 (Dilworth$\Rightarrow$Hall).

As the necessity of the condition is trivial, we show sufficiency:

Given sets $A_i$ satisfying condition (1), Let $Y=\{y_1,\mathrm{\dots },y_n\}$ be $n$ symbols representing the sets. We create a poset $P$ in the following way: The elements of $P$ is the disjoint union $X\cup Y$. The only relations are that $x\le y_i$ iff $x\in A_i$.

Clearly $X$ is an antichain in $P$. Suppose $S$ is another arbitrary antichain and let $J=\{1\le j\le n\mid y_j\in S\}$. The antichain criterion imposes that $A(J)\cap S=\mathrm{\varnothing }$, so

$$\left|S\right|\le \left|J\right|+(\left|X\right|-\left|A(J)\right|)\le \left|X\right|$$

because of (1). That means $X$ is a maximal antichain, and by Dilworth’s theorem, $P$ can be partitioned into $\left|X\right|$ chains. As a chain cannot contain more than one point from $X$ or more than one point from $Y$, the pigeonhole principle implies that each chain contains exactly one point from $X$ and at most one point from $Y$. Suppose that $x_i\in X$ is the element that is together with $y_i\in Y$ in a chain. Then $x_i\le y_i$, and thus $x_i\in A_i$, so $\{x_1,\mathrm{\dots },x_n\}$ is a SDR.

As an example of the use of this theorem we consider the following theorem due to G. Birkhoff. A matrix $M\in {\mathbb{Z}}_{\ge 0}^{n\times n}$ with nonnegative entries is called doubly statistic if every row and every column of $M$ has the same row/column sum.

Corollary 31.

A doubly statistic matrix $M=(m_{ij})$ with row/column sum $l$ can be written as the sum of $l$ permutation matrices.

Proof 1.2.

We define sets $A_i$, corresponding to the row indices by $A_i=\{j\mid m_{ij}>0\}$. For any $k$-tuple $K$ of indices, the sum of the corresponding rows of $M$ is $kl$. As every column of $M$ has column sum $l$, this means that these $k$ rows must have nonzero entries in at least $k$ columns, that is $\left|{\bigcup }_{i\in K}{A}_i\right|\ge k$. Thus 1 is satisfied and there is a SDR. We set $p_{i,j}=1$ if $j$ is the chosen representative for $A_i$ (and $p_{i,j}=0$ otherwise). Then $P=(p_{i,j})$ is a permutation matrix and $M-P$ is doubly statistic with sum $l-1$. The statement follows by induction on $l$.

2 Kőnig’s Theorems – Matchings

Eventually everything connects - people, ideas, objects…the quality of the connections is the key to quality per se. Charles Eames

Let $A$ be an $m\times n$ matrix with $0/1$ entries. A line of $A$ is a row or column. A set of lines covers $A$, if every nonzero entry of $A$ lies on at least one of the lines. Nonzero entries are called independent if no two lie on a common line. The term rank of $A$ is the maximum number of independent entries of $A$.

The following theorem is reminiscent of the properties of a basis in linear algebra:

Theorem 32 (Kőnig-Egerváry).

The minimum number of lines covering $A$ equals the term rank of $A$.

Let

Then $A$ can be covered with $3$ lines, and has an independent set of cardinality $3$.

Proof 2.1 (Hall$\Rightarrow$Kőnig-Egerváry).

Given $A\in {\{0,1\}}^{m\times n}$, let $p$ be the term rank of $A$ and $q$ the minimum number of lines covering $A$. We have to show that $p=q$.

We first show that $p\le q$: A cover of $l$ lines can cover at most $l$ independent $1$’s (no line covers more than one) but we can cover all ones with $q$ lines, so $p\le q$.

To see that $p\ge q$, without loss of generality permute the rows and columns of $A$ such that a minimal cover involves the first $r$ rows and the last $s$ columns of the matrix. We aim to find an independent set that has $r$ entries in the first $r$ rows and in columns $1,\mathrm{\dots },n-s$, and $s$ entries in the last $s$ columns in rows $r+1,\mathrm{\dots },m$:

For a row index $1\le i\le r$ let $N_i=\{1\le j\le n-s\mid A_{i,j}=1\}$. Then the union of any $k$ of these $N_i$’s contains at least $k$ column indices – otherwise we could replace these $k$ rows with columns in a minimal cover. By Hall’s theorem we thus have an SDR $\{x_1,\mathrm{\dots },x_r\}$. By definition $x_i\in N_i$ implies that $A_{i,x_i}=1$. Let $S=\{(i,x_i)\mid i=1,\mathrm{\dots },r\}$. Since the $x_i$ are distinct, this is an independent set.

A dual argument for the last $s$ columns gives an independent set $T$ of positions in the last $s$ columns and rows $r+1,\mathrm{\dots },n$. Since no position in $S$ shares row or column index with any position in $T$, $S\cup T$ also is an independent set, of cardinality $r+s=q$.

We reformulate this theorem in the language of graphs. A graph is called bipartite, if its vertex $V$ set can be written as a disjoint union $V=V_1\cup V_2$, so that no vertex in $V_i$ has a neighbor in $V_i$ (but only neighbors in $V_{3-i}$). A vertex cover in a graph is a set of vertices that every edge is incident to at least one vertex in the cover. A matching in a graph is a set of edges such that no two edges are incident to the same vertex. A matching is called maximal, if no matching with a larger number of edges exists.

We assume that the graphs we consider here have no isolated vertices.

Theorem 33 (Kőnig).

In a bipartite graph without isolated vertices, the number of edges in a maximum matching equals the number of vertices in a minimum vertex cover.

Figure 1 shows a bipartite graph with a maximum matching (bold).

Figure 1: A bipartite graph with maximum matching and minimum vertex cover.

Proof 2.2 (Kőnig-Egerváry$\Rightarrow$Kőnig).

Let $W,U\subset V$ be the two parts of the bipartition of vertices. Suppose $\left|W\right|=m$, $\left|U\right|=n$. We describe the adjacency in an $m\times n$ matrix $A$ with $0/1$ entries, $A_{i,j}=1$ iff $w_i$ is adjacent to $u_j$. (Note that the examples for this and the previous theorem are illustrating such a situation.)

A matching in the graph corresponds to an independent set — edges sharing no common vertices. A vertex cover — vertices such that every edge is incident — correspond to a line cover of the matrix. The result follows immediately from the Kőnig-Egerváry theorem.

Matchings in bipartite graphs can be interpreted as creating assignments between tasks and operators, between customers and producers, between men and women, etc., and thus clearly have practical implications (Compare the Marriage Theorem interpretation of Hall’s theorem!)

Due to this practical relevance, there is obvious interest in an algorithm for finding maximum matchings in a bipartite graph, the Assignment problem. The first algorithm published uses Kőnig’s theorem as a criterion whether an existing matching can be improved. Due to the origin of the theorem authors, it has been named the Hungarian Method. (It turns out that this method had been discovered before independently by Jacobi [jacobiassign].)

Let $M\subset E$ be a (not necessarily maximal) matching in a graph $\mathrm{\Gamma }=(V,E)$. We call an edge matched if it is in $M$, and free otherwise. Similarly, vertices incident to matched edges are called matched, vertices not incident to any matched edge are free.

An augmenting path for $M$ is a path whose end points are free and whose edges are alternatingly matched and free. This means all vertices but the end points are matched. Such a path allows us to replace $M$ with a larger matching, in that we can replace the matched edges of the augmenting path in $M$ with the free edges in the path, of which there is one more.

If the cardinality of $M$ is that of a vertex cover $C$, of course no augmenting paths can exist: Every edge of $M$ will be incident with exactly one vertex in $C$, leaving one of the two free edges at the end of the path without cover.

But if the cardinality is smaller there must be an augmenting path:

Corollary 34.

If for a vertex cover $C$, there either is a vertex cover of smaller size, or there is an augmenting path for $M$.

Figure 2: The two reduction in Corollary 34. Shaded area is cover.

Proof 2.3.

We prove the statement by induction over the number of vertices $\left|V\right|$, the base case being trivial.

Case 1: Assume that two vertices $v,w\in C$ are connected by an edge in $M$. Then both $v$ and $w$ must be incident to other edges, as we otherwise could drop one of them from $C$ and obtain a strictly smaller cover.

Furthermore one such edge $\{v,v_1\}$ must be to a vertex $v_1\notin C$ (as we otherwise could drop $v$ from the vertex cover). Clearly $\{v,v_1\}$ is free. We similarly find a free edge $\{w,w_1\}$ to a vertex $w_1\notin C$. If both $v_1$ and $w_1$ are free, then $v_1,v,w,w_1$ is an augmenting path. Otherwise at least one vertex, WLOG $v_1$, is matched thus incident to an edge $\{v_1,v_2\}\in M$. As we assumed that $v_1\notin C$ this implies that $v_2\in C$. As the graph is bipartite we also know that $v_2\ne w$. Now consider the smaller graph ${\mathrm{\Gamma }}^{\prime }$ obtained from $\mathrm{\Gamma }$ by deleting $v$ and $v_1$ (and the adjacent edges) and adding an edge $\{v_2,w\}$ if it did not yet exist. Then $M^{\prime }=(M-\{\{v,w\},\{v_1,v_2\}\})\cup \{\{v_2,w\}$ is a matching in ${\mathrm{\Gamma }}^{\prime }$ and $C^{\prime }=C-\{v\}$ a vertex cover in ${\mathrm{\Gamma }}^{\prime }$ (see Figure 2, left). By induction, we can either obtain a strictly smaller vertex cover $D$ for ${\mathrm{\Gamma }}^{\prime }$ (in which case $D\cup \{v\}$ or $D\cup \{v_1\}$ is a strictly smaller cover for $\mathrm{\Gamma }$), or an augmenting path for ${\mathrm{\Gamma }}^{\prime }$. If this path uses the new matching edge $\{v_2,w\}$, we replace this edge by the edge sequence $\{v_2,v_1\},\{v_1,v\},\{v,w\}$ and obtain an augmenting path in $\mathrm{\Gamma }$. This completes case 1.

In Case 2, we now may assume that no two vertices of the cover are connected by an edge in the matching, as $\left|M\right|\le \left|C\right|$ there must be an unmatched vertex $v\in C$.

If $v$ is adjacent to any other unmatched vertex this is an augmented path of length $1$.

Otherwise $v$ is adjacent to a matched vertex $w\notin C$ (if all neighbors are in $C$, we could remove $v$ from $C$). By a matched edge, $w$ is adjacent to another vertex $x$, and to cover that edge we must have $x\in C$. We furthermore may assume that $w$ was chosen so that $x$ is also incident to an edge not in the matching, as we otherwise could replace all $x$’s with the respective $w$’s in the cover and remove $v$ from $C$, reducing the cover size.

Now consider the graph ${\mathrm{\Gamma }}^{\prime }$, obtained by removing the vertices $v$ and $w$ and their incident edges and set $M^{\prime }=M\setminus \{\{x,w\}\}$ and $C^{\prime }=C\setminus \{v\}$ (Figure 2, right).

Then $C^{\prime }$ is a vertex cover of ${\mathrm{\Gamma }}^{\prime }$ (all edges that $v$ covered are gone). Also $M^{\prime }$ is a matching with . By induction, either ${\mathrm{\Gamma }}^{\prime }$ has a smaller cover $D$ (in which case $D\cup \{v\}$ is a smaller cover for $\mathrm{\Gamma }$), or there is an augmenting path. If this path imvolves $x$, we extend it by $xwv$ and thus obtain an augmenting path for $\mathrm{\Gamma }$.

To find a maximal matching, one can thus simply start with some arbitrary matching (pick edges as long as no two share a vertex) and vertex cover and then use corollary 34 to refine them iteratively.

It is not hard to generalize this approach to (complete) bipartite graphs with weighted edges to obtain a (perfect: all vertices are matched) matching of maximal weight (profit):

Given an arbitrary matching with weighted edges, replace an edge $\{a,b\}$ with (assume: integral) weight $w$ by a set of edges $\{a,b_1\},\{b_1,a_2\},\{a_2,b_2\},\mathrm{\dots },\{a_w,b\}$ with newly introduced vertices $a_i,b_i$ that are not connected in any other way. Selecting the edge $\{a,b\}$ in the original graph thus now allows selection of $w$ edges. Thus the maximum weight of a matching in the original graph corresponds to the cardinality of a maximum matching in the new graph.

1 Stable Matchings

…to Alvin E. Roth and Lloyd S. Shapley “for the theory of stable allocations and the practice of market design”. Citation for the Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel 2012

Also of practical interest is the concept of a stable matching (or stable marriage). Imagine a matching in a bipartite graph represents an assignment of students to college places. Every student has a personal preference ranking of colleges, every college (place – assume for simplicity that every college just has one student) has a personal ranking of students. A matching is instable (otherwise: stable), if there is a student $s$ and a college $c$ such that $s$ ranks $c$ higher than their current college, and $c$ ranks $s$ higher than their current student.

A priori it is unclear that stable matchings exist, the following algorithm not only proves that but also gives a way of producing one:

[Deferred Acceptance, Gale, Shapley] Every student has a temporarily assigned college, colleges may have a temporarily assigned student. Once a college has been assigned a student, it will replace it only by one it ranks higher. A student may be moved down from higher ranked to lower ranked colleges.

For bookkeeping, students carry a rejected label that will change status as the algorithm goes on, and also and carry for each college an indicator whether they have been rejected by this college.

1. [Initialize] Label every student as rejected

2. [Complete] If no student is rejected, terminate.

3. [Student Choice] Every student marked as rejected applies to the college she ranks highest amongst those who have not yet rejected her.

4. [College Choice] Every college tentatively picks from the students who chose it the one it ranks highest (and removes that students rejection status). It rejects all other students who have selected it,even if they had been picked tentatively before.

5. Go back to step 2.

Proof 2.4.

The only way the process terminates is if no student is rejected, that is they were tentatively accepted by a college and this college has no student applying it would rank higher. All colleges which the student ranks higher have rejected her because they were able to accept a student they rank higher, so the matching is stable.

In every round, students select from colleges and are either tentatively accepted, or are left with colleges of lower preference. As there is a finite set of students and preferences, this process must terminate.

This algorithm is used for example in the US to match graduating medical doctors to hospital training positions, www.nrmp.org. It also was instrumental for the award of the 2012 Nobel prize in Economics to Shapley and Roth.

3 Menger’s theorem

Live in fragments no longer. Only connect, and the beast and the monk, robbed of the isolation that is life to either, will die. Howards End
E. M. Forster

Kőnig’s aim in proving the Theorem 33 was as a tool towards a proof for a more general theorem by Menger that deals with connections in a graph (and gets us in statement and proof back close to Dilworth’s theorem), but whose proof, when first published, turned out to not work in the case of bipartite graphs.

Let $u,w$ be nonadjacent vertices in a graph $\mathrm{\Gamma }$. A $uw$-vertex path in $\mathrm{\Gamma }$ is a path from $u$ to $w$. A collection of $uw$-vertex paths is called independent, if the paths are pairwise disjoint except for $u$ and $w$. A set $S$ of vertices, excluding $u$ and $w$, is $uw$-vertex separating, if every $uw$ path must contain a vertex of $S$. Clearly the minimum cardinality of a $uw$ vertex separating set must be at least as large as that of a number of $uw$ independent paths. It turns out that they are equal:

Theorem 35 (Menger).

Let $u,w$ be nonadjacent vertices in a graph. Then the maximum number of independent $uw$ vertex paths equals the minimum cardinality of a $uw$ vertex separating set.

As Kőnig’s proof is comparatively long, we will instead give a direct proof due to G. Dirac. Note the similarity to the proof of Dilworth’s theorem!

Proof 3.1.

Let $m$ be the minimum cardinality of a separating set, and $M$ the maximum number of independent paths. We have seen that $m\ge M$.

Assume that the theorem is false and $\mathrm{\Gamma }=(V,E)$ be a graph with a minimum number of edges for which the theorem fails, that is we have two nonadjacent vertices $u$ and $w$ and fewer than $m$ independent vertex paths.

If $e$ is an edge not incident to $u$ or $w$, we can remove $e$ and obtain a smaller graph $\mathrm{\Delta }$ for which the theorem holds. Since $\mathrm{\Gamma }$, and thus $\mathrm{\Delta }$ has at most $m-1$ $uw$-independent paths this means that in $\mathrm{\Delta }$ there is an $uw$-separating set $T$ of size $m-1$. If we add one of the vertices incident to $e$ to this set $T$, we obtain a set $S$ of cardinality $m$ which is $uw$ separating – any path connecting in $\mathrm{\Gamma }$ but not in $\mathrm{\Delta }$ clearly would have to use the edge $e$. We thus may assume that $S$ contains a vertex not adjacent to $u$ or $w$.

Next, we note that there is no path $usw$ with $s\in S$ of length $2$ – if there was we could remove $s$ and have a graph with fewer edges and $m-1$ separating vertices and less than $m-1$ independent paths, contradicting the minimality of $\mathrm{\Gamma }$.

For the final contradiction, denote by $P_u$ the set of vertex paths between $u$ and exactly one vertex in $S$ and $P_w$ ditto for $w$. The paths in $P_u$ and $P_w$ have only vertices of $S$ in common (otherwise we could circumvent $S$, contradicting that it is separating).

We claim that all vertices of $S$ are adjacent to $u$, or that all vertices in $S$ are adjacent to $w$. This will contradict the choice of $S$ and prove the theorem:

Consider the graph consisting of $P_u$, $w$ and edges $sw$ for $s\in S$. If $w$ is not adjacent to all vertices in $s$, this graph has fewer edges than $G$, so by assumption has $m$ independent paths from $u$ to $w$. If we leave out the $sw$-step from these paths we obtain a set $R_u$ of $m$ independent paths from $u$ to the $m$ elements of $S$. Similarly, we get a set of independent paths $R_w$ from $w$ to the elements of $S$. Combining these paths at the elements of $s$ yields $m$ independent paths from $u$ to $w$, contradiction.

A dual version of the theorem holds for disjoint paths:

Theorem 36 (Menger’s theorem, edge version).

The maximum number of edge-disjoint paths from $u$ to $w$ equals the minimum number of edges, whose removal would put $u$ and $v$ into disjoint components.

The proof of the theorem is by the ordinary version, applied to the line graph $L(\mathrm{\Gamma })$ of $\mathrm{\Gamma }$. The vertices of $L(\mathrm{\Gamma })$ are the edges of $\mathrm{\Gamma }$, two vertices are adjacent if the edges in $\mathrm{\Gamma }$ are incident to the same vertex. See figure 3 for an example.

Figure 3: A graph and its line graph

Menger’s theorem also generalizes in the obvious way to directed graphs, though we shall not give a statement or proof here.

4 Network Flows, Max-flow/Min-cut

And he thought of himself floating on his back down a river, or striking out from one island to another, and he felt that that was really the life for a Tigger. The house at Pooh corner
A. A. Milne

A network is a digraph $(V,E)$ with weighted edges with two distinguished vertices, the source $s$ and the target $t$. We assume that the weights (which we call capacities) $c:E\to {ℝ}_{\ge 0}$ are nonnegative. (Below we shall assume that weights are in fact rational – clearly we can approximate real weights to arbitrary precision. We shall investigate the issue of irrational capacities in the exercises.) An example is given in Figure 4. For a (directed) edge $e=(a,b)$ we denote by $\iota (e)=a$ the initial, and by $\tau (e)=b$ the terminal vertex of this edge.

Figure 4: A network

The reader might want to consider this as a network of roads with weights being the maximal capacity. (It is possible to have different capacities in different directions on the same road.) We want to transport vehicles from $s$ to $t$ (and implicitly ask how many we can transport through the network).

Note that we are looking for a steady state in a steady-state transport situation; that is we do not want to transport once, but forever, and ask for the transport capacity per time unit.

A flow is a function $f$ defined on the edges (indicating the number of units we transport along that edge) such that

• $0\le f(e)\le c(e)\forall e\in E$ (do not exceed capacity).

• ${\sum }_{\iota (e)=v}f(e)={\sum }_{\tau (e)=v}f(e)\forall v\in V\setminus \{s,t\}$ (No intermediate vertex can buffer capacity or create new flow. This is Kirchhoff’s law in Physics.)

The value of a flow is the net transport out of the source:

$$\text{val}(f)=\sum _{\iota (e)=s}f(e)-\sum _{\tau (e)=s}f(e).$$

This definition might seem asymmetric in focusing on the source, however Lemma 4.1 will show that this is a somewhat arbitrary choice.

The question we ask thus is for the maximal value of a flow. The main tool for this is to consider the flow passing “by a point” in the network:

A cut $C\subset V$ in a network is a set of vertices such that $s\in C$, $t\notin C$. We do not require the cut to be connected, though in practice it usually will be.

We note that the value of any flow is equal to the net flow out of a cut. (This implies that the value of a flow also is equal to the net transport into the target):

Lemma 4.1.

Let $C$ be a cut. We denote the edges crossing the cut by

$C^o$ $=$ $\{e\in E\mid \iota (e)\in C,\tau (e)\notin C\},$

$C^i$ $=$ $\{e\in E\mid \tau (e)\in C,\iota (e)\notin C\}.$

Then for any flow $f$ we have that

$$\text{val}(f)=\sum _{e\in C^o}f(e)-\sum _{e\in C^i}f(e).$$

Proof 4.2.

We prove the statement by induction on the number of vertices in $C$. For $\left|C\right|=1$ we have that $C=\{s\}$ and the statement is the definition of the value of a flow.

Now suppose that $\left|C\right|>1$, let $s\ne v\in C$ and $D=C\setminus \{v\}$. By induction, the statement holds for $D$.

We now consider the following disjoint sets of edges:

$P^o$ $=$ $\{e\in E\mid \iota (e)\in D,\tau (e)\notin C\},$

$P^i$ $=$ $\{e\in E\mid \tau (e)\in D,\iota (e)\notin C\},$

$Q^o$ $=$ $\{e\in E\mid \iota (e)\in D,\tau (e)=v\},$

$Q^i$ $=$ $\{e\in E\mid \tau (e)\in D,\iota (e)=v\},$

$R^o$ $=$ $\{e\in E\mid \iota (e)=v,\tau (e)\notin C\},$

$R^i$ $=$ $\{e\in E\mid \tau (e)=v,\iota (e)\notin C\}.$

Any edge that starts at $v$ must be in $Q^i$ or in $R^o$, any edge ending at $v$ must be in $Q^o$ or in $R^i$. Kirchhoffs law thus gives us that

$$\sum _{e\in Q^i}f(e)+\sum _{e\in R^o}f(e)=\sum _{e\in Q^o}f(e)+\sum _{e\in R^i}f(e).$$

It is easily seen that $C^o=P^o\cup R^0$, $C^i=P^i\cup R^i$ and that $D^o=P^o\cup Q^o$ and $D^i=P^i\cup Q^i$. Therefore, using the previous expression to replace a difference of $Q$-sums by a difference of $R$-sums:

$\text{val}(f)$ $=$ ${\displaystyle \sum _{e\in D^o}}f(e)-{\displaystyle \sum _{e\in D^i}}f(e)$

$=$ ${\displaystyle \sum _{e\in P^o}}f(e)-{\displaystyle \sum _{e\in P^i}}f(e)+\underset{={\sum }_{e\in R^o}f(e)-{\sum }_{e\in R^i}f(e)}{\underbrace{{\displaystyle \sum _{e\in Q^o}}f(e)-{\displaystyle \sum _{e\in Q^i}}f(e)}}$

$=$ ${\displaystyle \sum _{e\in C^o}}f(e)-{\displaystyle \sum _{e\in C^i}}f(e).$

The claim follows by induction.

We define the capacity of a cut as the sum of the capacity of the edges leaving the cut:

$$\text{cap}(C)=\sum _{e\in C^o}c(e).$$

Lemma 4.1 thus implies that the value of any flow must be bounded by the capacity of any cut and thus (unsurprisingly) the maximal flow value is bounded by the minimum cut capacity – a chain is only as strong as its weakest link.

Similar to the dualities we considered before, equality is attained:

Theorem 37 (Max-Flow Min-Cut, integer version).

Suppose the capacity function $c$ in integer valued. Then the maximum value of a flow in a network is equal to the minimum capacity of a cut. Furthermore, there is a maximum flow $f$ that is integer valued.

Note 4.3.

If the capacity function is rational valued, we can simply scale with the lcm of the denominators and obtain an integer valued capacity function. In the case of irrational capacities, the theorem holds by a boring approximation argument.

Proof 4.4 (Menger$\Rightarrow$Max-flow).

Given a directed network, replace every arc with integral weight $c$ by $c$ disjoint directed edges.

Clearly, if one edge of a $c$-fold multi-edge set is in a minimum separating set, the other $c-1$ edges have to be.

Thus the cardinality of a minimum edge-separating set is a minimum cut, while $k$ independent paths give a flow of $k$. By the edge version of Menger’s theorem, the minimum cardinality of an edge-separating set equals the maximum number of independent edge paths, proving the theorem.

The existence of a maximum flow with integer values will follow from the following algorithm.

The algorithm of Ford and Fulkerson finds a maximal flow for a given network. It start with a valid flow (say $f(e)=0$ for all edges) and then improves this flow if possible, using the following main step: [increase flow] Given a flow $f$, return a flow with higher value, or show that no such flow exists.

1. Let $A:=\{s\}$. $A$ is a cut of vertices that can be supplied at higher rate from the source. $I:=\{\}$. $I$ is a set of edges that are not yet at capacity. $R:=\{\}$. $R$ is a set of edges whose flow should be reduced.

2. If $t\in A$, go to step 6.

3. If there is an edge $e\in A^o$ with , set $A:=A\cup \{\tau (e)\}$, $I:=I\cup \{e\}$. Go to step 2.

4. If there is an edge $e\in A^i$ with $f(e)>0$ This is flow into $A$ which we could reduce, set $A:=A\cup \{\iota (e)\}$, $R:=R\cup \{e\}$. Go to step 2.

5. If neither of these two properties hold, terminate with a message that the flow is maximal.

6. By tracing back how $t$ got added to $A$, we construct an (undirected) path (the augmenting path) $P=(e_1,e_2,\mathrm{\dots })$ from $s$ to $t$. Let

   $$d=\min (\underset{e\in P\cap I}{\min }(c(e)-f(e)),\underset{e\in P\cap R}{\min }f(e)).$$

   Increase the flow on $P\cap I$ by $d$, reduce the flow on $P\cap R$ by $d$. This satisfies Kirchhoffs law. Return the larger flow.

Proof 4.5.

We shall show termination in the case of integral capacities: Every time we adjust a flow, we may assume that the flow on one edge increases by an integral value. This can only happen a finite number of times.

Once the algorithm ends in step 5, we have a cut $A$ such that ${\sum }_{e\in A^i}f(e)=0$, ${\sum }_{e\in A^o}f(e)={\sum }_{e\in A^o}c(e)$, thus $\text{val}(f)=\text{cap}(A)$ and the flow must be maximal by Theorem 37.

We illustrate the algorithm in the example from above. Figure 5, a) shows some flow (in blue). The total flow is 24.

We start building the list of under-supplied vertices and mark edges on which to increase, respectively reduce the flow:

Vertices	Increase	Reduce
s
B	sB
A		AB
D	AD
t	DT

We find an augmenting path sBADt (red in Figure b) and note that we can increase the flow by 2 (the limiting factor being edge sB) to a total of 26.

Starting again, we obtain (Figure c) the augmenting path sCFBAEt, on which we can increase the flow by 2 again, resulting is a flow of 28.

Finally we build the under-supplied cities as C,F,B and then cannot increase the set. Thus (Figure d), shaded) $\{s,C,F,B\}$ is a cut whose capacity of 28 is reached, proving that we have a maximal flow.

a) b)

c) d)

Figure 5: Increasing a given flow to maximum

Figure 6: Example for bad augmenting paths

Note 4.6.

As given, the algorithm is not necessarily in polynomial time, as there might be a huge number of small incremental steps. Take the network in Figure 6. Starting with a flow of 0, we choose the augmenting path sABt on which we can increase the flow by 1. Next, we take the augmenting path sBAt, reducing the flow on AB to 0 again and have a total flow of 2. We can iterate this, increasing the flow by 1 each step until we get the maximum flow of 200.

Polynomial time in this algorithm however can be achieved by a more careful choice of the augmenting path (e.g. a shortest path, Edmonds-Karp algorithm), that analysis however is beyond the scope of these notes.

Note 4.7.

To close the circle, observe that the Max-flow/Min-cut theorem implies Dilworth’s theorem: Given a poset, we model it as a directed network with flow from bottom to top and arc capacity one. Thus all theorems mentioned in this section (and in fact a few more we have not mentioned) are in a sense mutually equivalent and form the fundamental theorem of discrete optimization.

1 Braess’ Paradox

On Earth Day this year, New York City’s Transportation Commissioner decided to close 42d Street, which as every New Yorker knows is always congested. ”Many predicted it would be doomsday,” said the Commissioner […] But to everyone’s surprise […] Traffic flow actually improved when 42d Street was closed. New York Times, 12/25/1990, p.38
Gina Kolata

From the time of Say and Ricardo the classical economists have taught that supply creates its own demand The General Theory of Employment, Interest, and Money
John Maynard Keynes

Often the question of maximal flow turns up not just for an existing network, but already at the stage of network design, aiming to maximize flow. Braess’ paradox shows that this can be very nonintuitive.

While we shall give a theoretical example, concrete instances of this effect have been observed in the real world in several cities (New York; Stuttgart, Germany; Winnipeg, Canada;…) when roads had been temporarily blocked because of building work, or after new roads were built. The interested reader might observe obvious implications to society and politics.

Suppose we have four cities, A, B, C, D with connecting roads as shown in figure 7, left. The reader may observe that this configuration is similar to the one in Note 4.6.

Cities A and B as well as C and D are connected by a minor road which easily clogs up. The driving time thus depends strongly on the number of cars, it is

$$t_{AB}=t_{CD}=10x.$$

with $x$ the number of drivers in thousands. An obstacle blocks direct connections from B to C.

Figure 7: Braess’ paradox: Before and after a new road is built.

High capacity roads have been build to connect A and C, as well as B and D. While overall time is longer, the impact for extra cars is less. Driving time with $x$ thousand drivers on the road is

$$t_{AC}=t_{BD}=50+x.$$

Assume 6000 drivers want to travel from $A$ to $D$. A symmetry argument shows that half (3000) travel via $B$ and half via $C$. Their individual travel time is $10\cdot 3+50+3=83$. It is not hard to show that this is a stable equilibrium, i.e. no traveler can gain by changing their route. Furthermore, the system will settle in this equilibrium by itself, as long we assume drivers want to minimize their travel time and when starting their journey have perfect knowledge of how many cars are on each road.

Eventually, a new connection is built from B to C through the obstacle (right image). (For simplicity of the argument we shall assume that it is one-way, but that is not crucial for the paradox, but only simplifies analysis.) It has high capacity and is short, so travel time on this route is

$$t_{BC}=10+x.$$

We now have three possible routes from $A$ to $D$: $ABD$, $ACD$, and $ABCD$. Again assuming perfect information, drivers will move towards a distribution in which travel time along all possible routes is equal. We claim that such an equilibruum exists with 2000 drivers each using $ABD$, $ACD$ and $ABCD$. (This means that 4000 drivers are traveling AB and CD, respectively, 2000 travel BC.) This is because we have

$t_{ABD}$ $=$ $=10\cdot 4+(50+2)=92$

$t_{ABCD}$ $=$ $10\cdot 4+(10+2)+10\cdot 4=92$

$r_{ACD}$ $=$ $(50+2)+10\cdot 4=92.$

Again, one can show that this is the only equilibruum, and that it is stable.

But this new optimal travel time is $92>83$ and thus more than before. Implications that this might have for society are left to the reader as an exercise.

Some Counting Sequences

Bell

OEIS A000110, page 7
$B_0=1,B_1=1,B_2=2,B_3=5,B_4=15,B_5=52,B_6=203,B_7=877,B_8=4140,B_9=21147,B_{10}=115975$

Catalan

OEIS A000108, page 9
$C_0=1,C_1=1,C_2=2,C_3=5,C_4=14,C_5=42,C_6=132,C_7=429,C_8=1430,C_9=4862,C_{10}=16796$

Derangements

OEIS A000166, page 5
$d(0)=1,d(1)=0,d(2)=1,d(3)=2,d(4)=9,d(5)=44,d(6)=265,d(7)=1854,d(8)=14833$

Involutions

OEIS A000085, page 10
$s(0)=1,s(1)=1,s(2)=2,s(3)=4,s(4)=10,s(5)=26,s(6)=76,s(7)=232,s(8)=764$

Fibonacci

OEIS A000045, page 2
$F_0=1,F_1=1,F_2=2,F_3=3,F_4=5,F_5=8,F_6=13,F_7=21,F_8=34,F_9=55,F_{10}=89,F_{11}=144$

Partitions

OEIS A000041, page LABEL:partdef
$p(0)=1,p(1)=1,p(2)=2,p(3)=3,p(4)=5,p(5)=7,p(6)=11,p(7)=15,p(8)=22,p(9)=30$