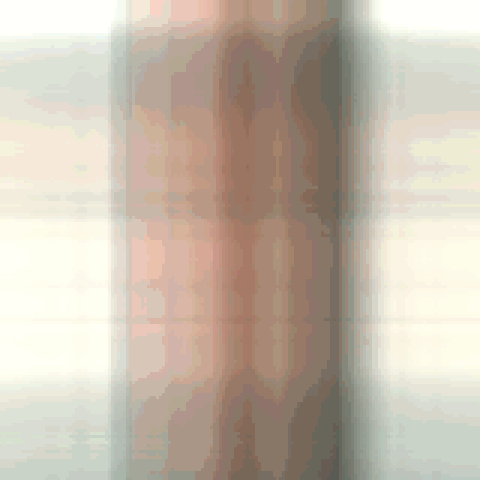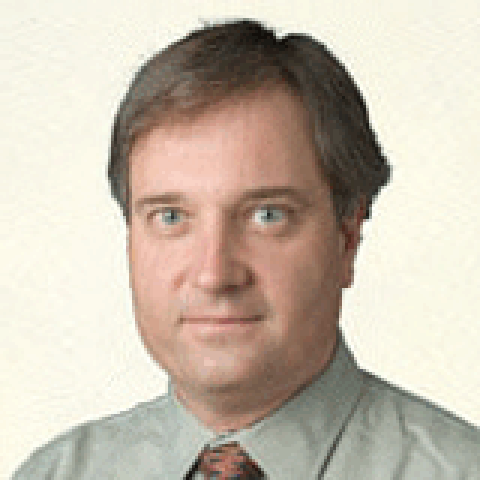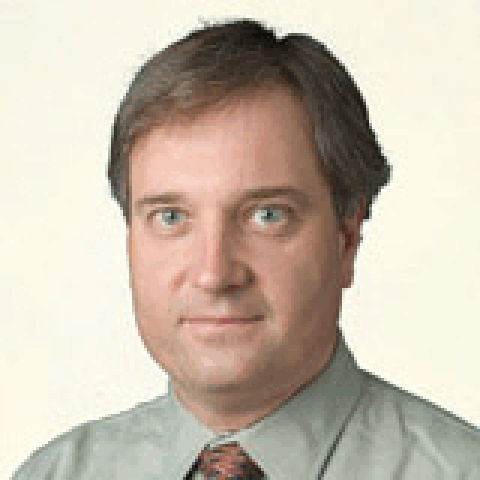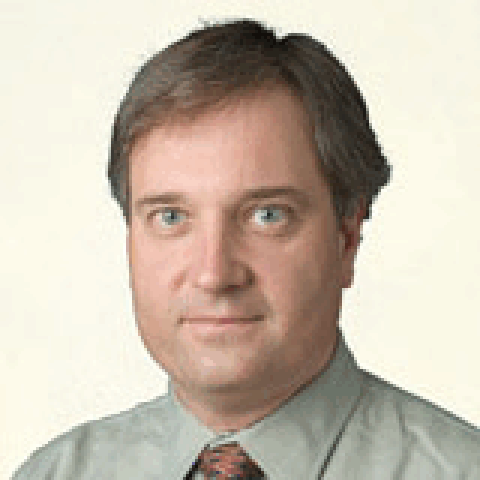Picture Processing with Linear Algebra

Low rank approximation for Lossy compression

We can consider a grayscale digital picture as a matrix A with entries in a fixed interval given by brightness levels. (As the picture is in fact in color the same has been done for the red, green and blue component and the results have been overlayed.)
We now form the singular value decomposition A=U·S·V with U and V orthogonal and S diagonal with the sigular values on the diagonal in descending order.

If we now form a product U·T·V, where T is a matrix obtained from S by zeroing out all but the largest diagonal entries, then this product can be considered as a low-rank approximation of A.

The picture on the side shows this process animated with rank 1, rank 2 etc. approximations. Somewhat surprisingly even a rather low rank approximation produces a decent picture.