From Obtuse Triangles to DNA Models and Synthetic Polymers
The Geometry of Random Polygons

Lewis Carroll's Pillow Problem #58
Random Points on an Infinite Plane
Probability \(p\)
\(p\)
\(p\)
\(p\)
\(p\)
Uh oh!
In Fact...
There is no way to choose points randomly in the plane so that the probability that a point lies in a region depends only on the size of the region.
Fancier Version
The uniform measure on the plane is not a probability measure.
Gaussians to the Rescue?
One way to choose points randomly in the plane is according to the Gaussian (normal) distribution.
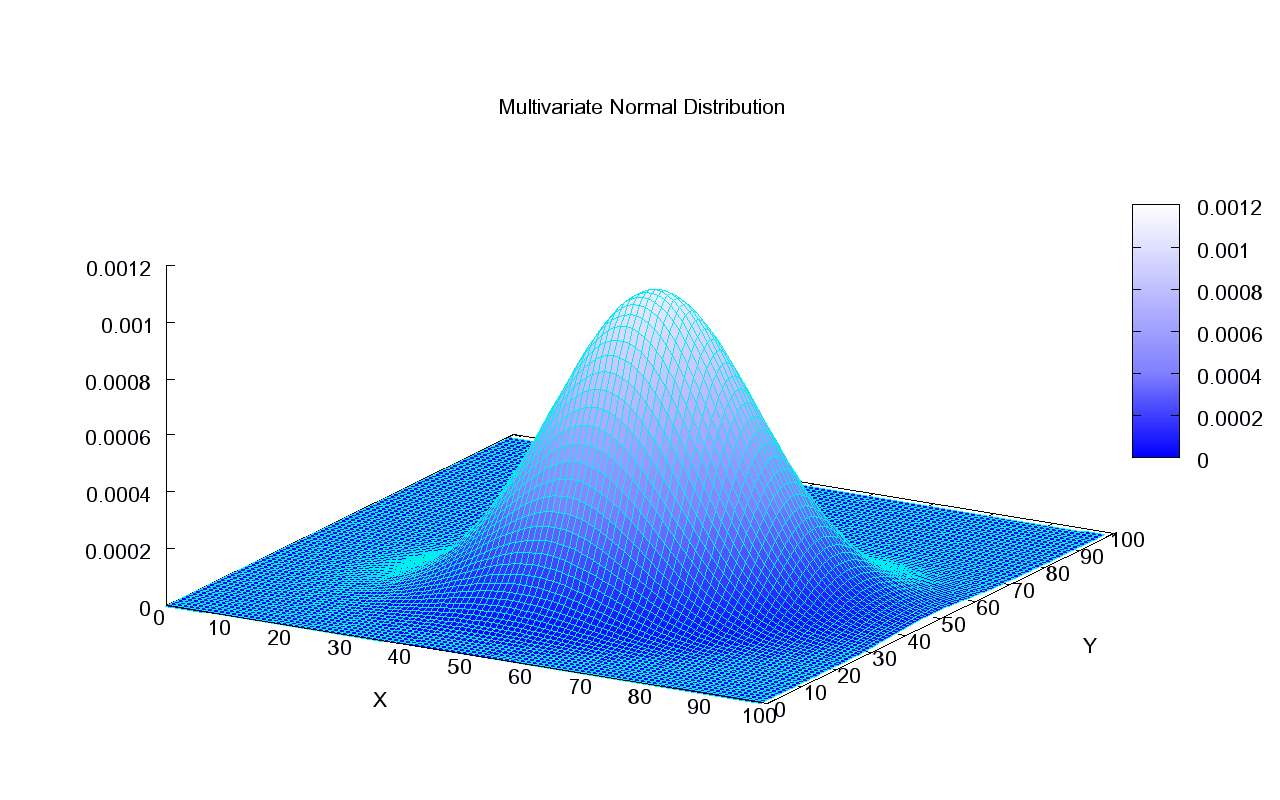
Proposition: Suppose the vertices \((x_1,y_1),(x_2,y_2),(x_3,y_3)\) of the triangle are chosen independently from the standard 2-variable Gaussian distribution. Then
\(\mathbb{P}(\text{obtuse})=\frac{3}{4}\)
Choose three vertices uniformly in the disk:
\(\mathbb{P}(\text{obtuse})=\frac{9}{8}-\frac{4}{\pi^2}\approx 0.7197\)
Restricted Domain?

Choose three vertices uniformly in the square:
\(\mathbb{P}(\text{obtuse})=\frac{97}{150}-\frac{\pi}{40}\approx 0.7252\)
Random Triangles?
Is Carroll’s question really about choosing random points, or is it actually about choosing random triangles?
How would you choose a triangle “at random”?
Carroll’s Answer
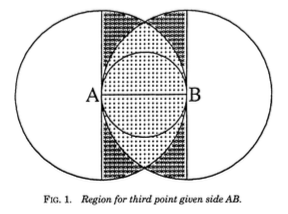
Suppose \(AB\) is the longest side. Then
\(\mathbb{P}(\text{obtuse})=\frac{\pi/8}{\pi/3-\sqrt{3}/4} \approx 0.64\)
But if \(AB\) is the second longest side,
\(\mathbb{P}(\text{obtuse}) = \frac{\pi/2}{\pi/3+\sqrt{3}/2} \approx 0.82\)
Angles?!
Remember from Geometry that three angles \((\theta_1,\theta_2,\theta_3)\) determine a triangle up to similarity (AAA).

\(\theta_1\)
\(\theta_2\)
\(\theta_3\)
What are the restrictions on the \(\theta_i\)?
\(\theta_1+\theta_2+\theta_3=\pi\)
\(0<\theta_1, 0 < \theta_2, 0<\theta_3\)
and
The Triangle of Triangles
\(\theta_1+\theta_2+\theta_3=\pi\)
\(0<\theta_1, 0 < \theta_2, 0<\theta_3\)
and
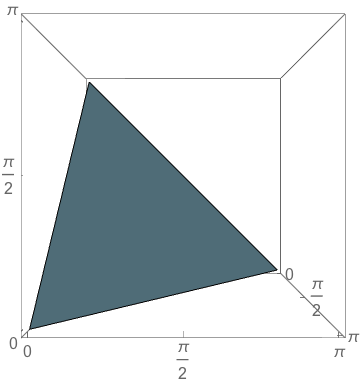
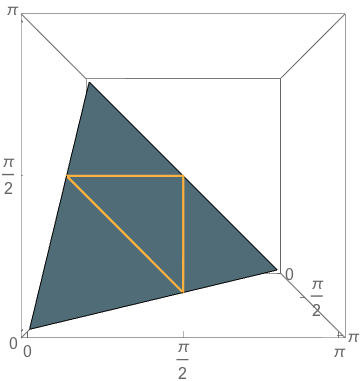
\(\theta_1=\pi/2\)
\(\theta_2=\pi/2\)
\(\theta_3=\pi/2\)
\(\mathbb{P}(\text{obtuse})=\frac{3}{4}\)
Side Lengths?!
Remember the sidelengths \((a,b,c)\) uniquely determine a triangle (SSS).
Obtuseness is scale-invariant, so pick a perimeter \(P\) and we have \(a+b+c=P\).
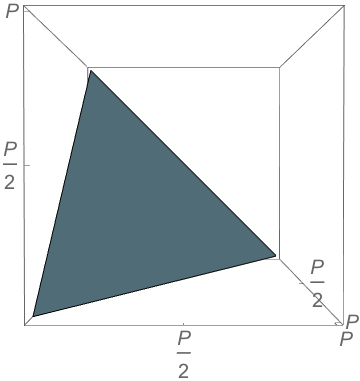
Problem
Not all points in the simplex correspond to triangles
\(b+c<a\)
\(a+b<c\)
\(a+c<b\)
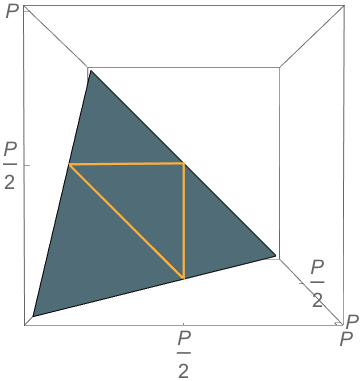
Yet Another Pillow Problem Answer
\(\mathbb{P}(\text{obtuse})=9-12\ln 2 \approx 0.68\)
\(b^2+c^2=a^2\)
\(a^2+b^2=c^2\)
\(a^2+c^2=b^2\)
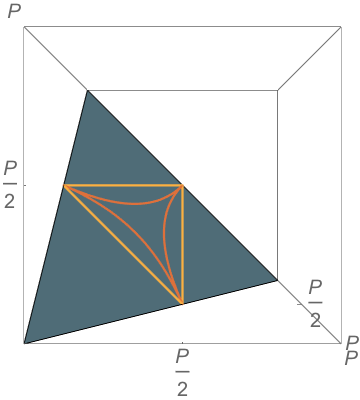

— Stephen Portnoy, Statistical Science 9 (1994), 279–284
Random Triangles...?
Translation for Geometers
The space of all triangles should be a (preferably compact) manifold \(T\) with a transitive isometry group. We should use the left-invariant metric on \(T\), scaled so vol\((T)=1\). Then the Riemannian volume form induced by this metric is a natural probability measure on \(T\), and we should compute the volume of the subset of obtuse triangles.
Ideally, this should generalize to \(n\)-gons.
Spoiler: \(T\simeq\mathbb{RP}^2=G_2\mathbb{R}^3\)
Back to Triangles
Let \(s=\frac{1}{2}(a+b+c)\) and define

Note: It’s convenient to choose \(s=1\).
\(s_a=s-a, \quad s_b = s-b, \quad s_c = s-c\)
Then
\(s_a+s_b+s_c=3s-(a+b+c)=3s-2s=s\)
and the triangle inequalities become
\(s_a>0, \quad s_b > 0, \quad s_c > 0\)
But there’s still no transitive group action!
Take Square Roots!
Consider \((x,y,z)\) so that
\(x^2=s_a, \quad y^2 = s_b, \quad z^2 = s_c\)
The unit sphere is a \(2^3\)-fold cover of triangle space

The Transitive Group
The rotations are natural transformations of the sphere, and the corresponding action on triangles is natural.
\(c=1-z^2\) fixed
\(z\) fixed
\(C(\theta) = (\frac{z^2+1}{2}\cos 2\theta, z \sin 2\theta)\)
The equal-area-in-equal-time parametrization of the ellipse
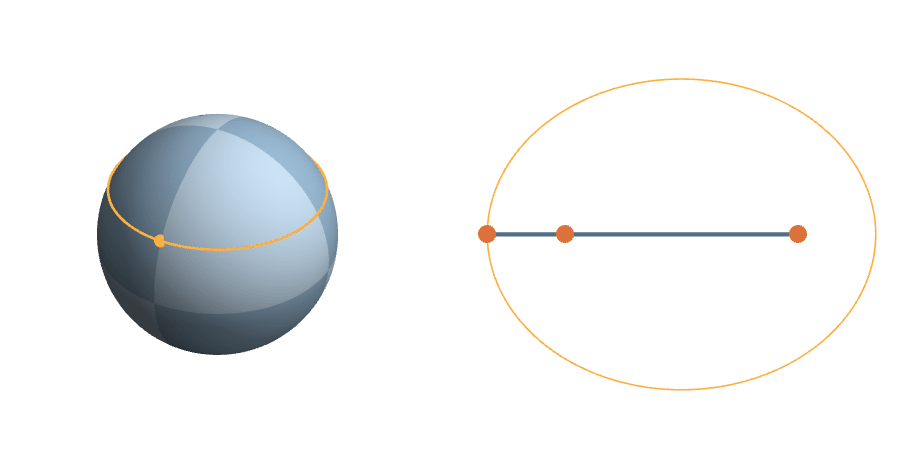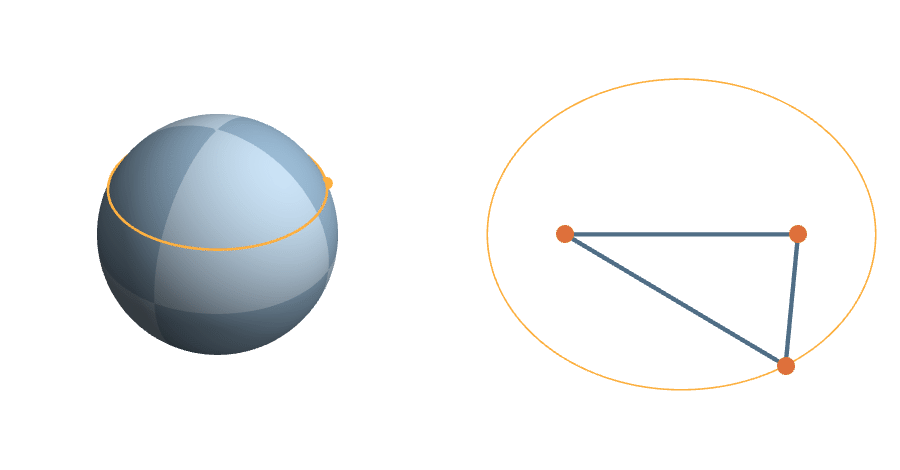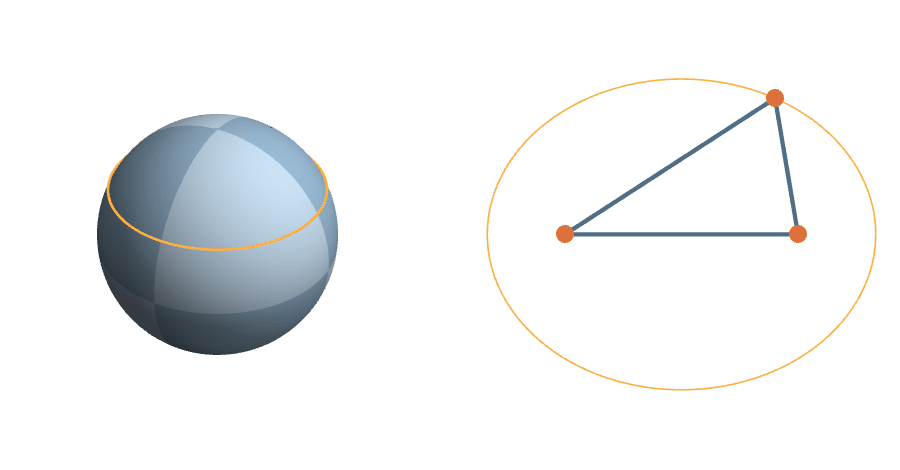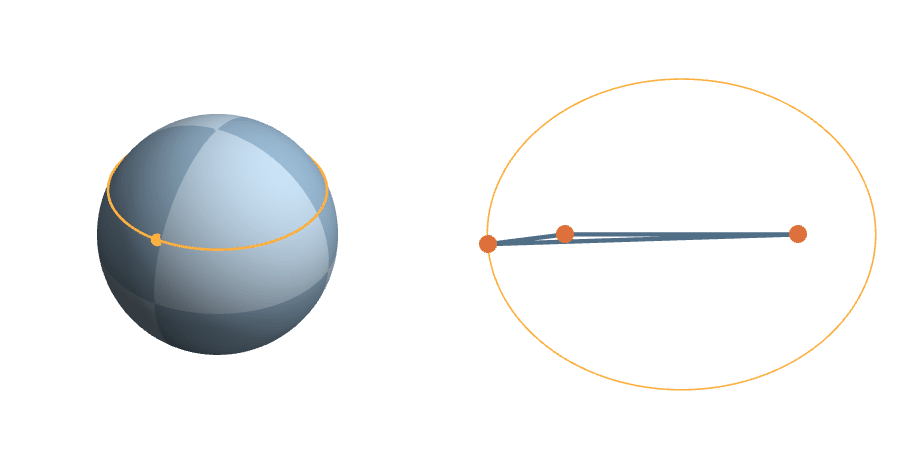
A More Complicated Rotation
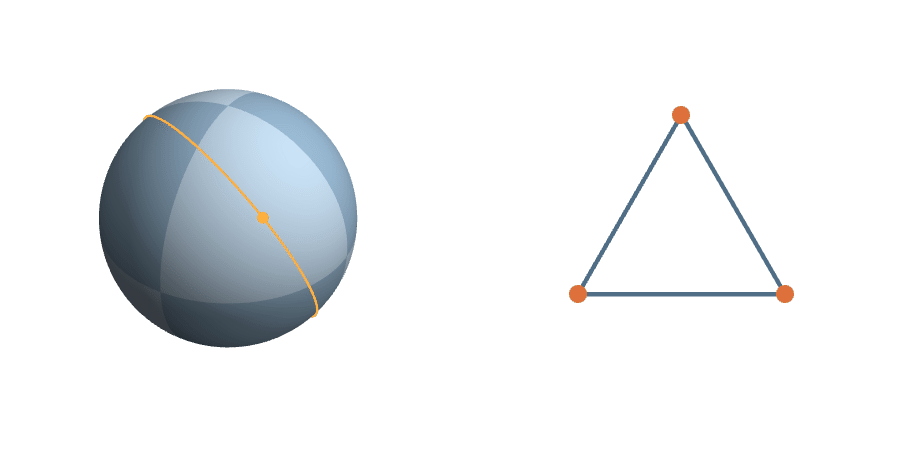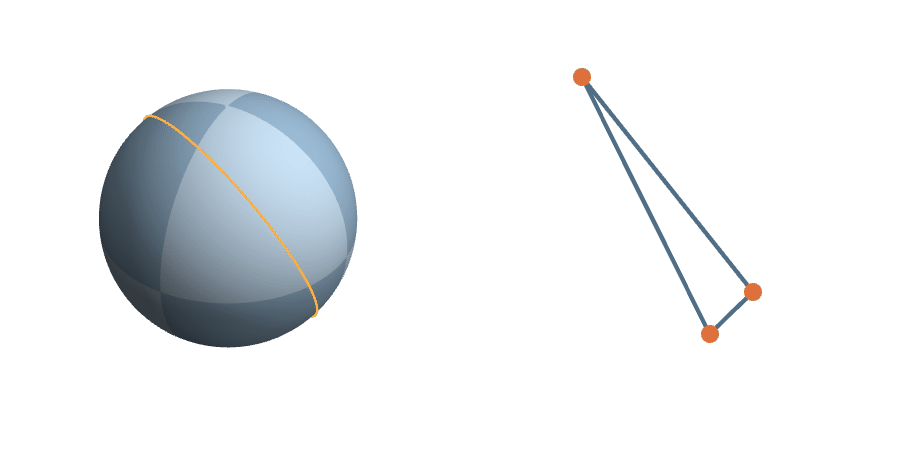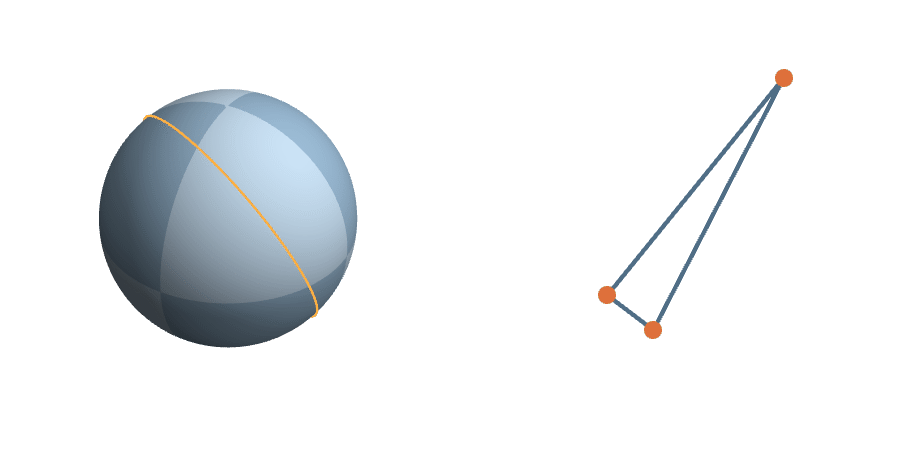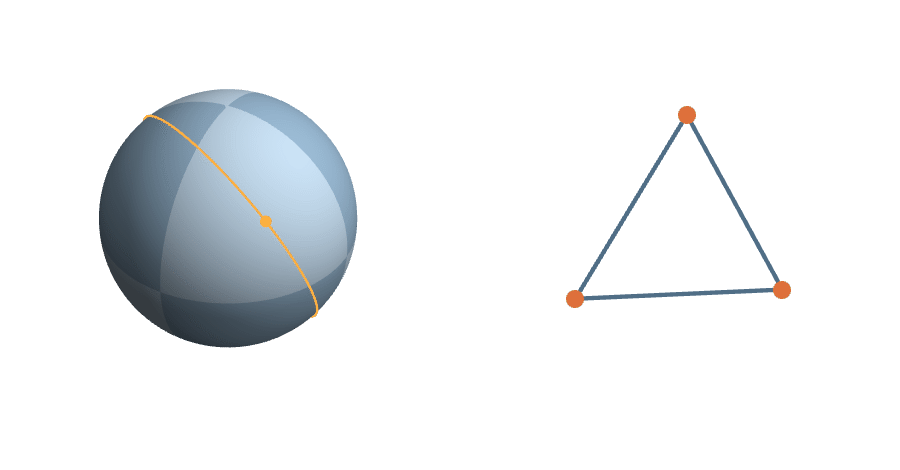
A Measure on Triangle Space
Since the uniform measure is the unique (up to scale) measure on \(S^2\) invariant under the action of \(SO(3)\)...
Definition
The symmetric measure on triangle space is the probability measure proportional to the uniform measure on the sphere.
408 random triangles
(collab. w/ A. Harding)
Right Triangles
The right triangles are exactly those satisfying
\(a^2+b^2=c^2\) & permutations
Since \(a=1-s_a=1-x^2\), etc., the right triangles are determined by the quartic
\((1-x^2)^2+(1-y^2)^2=(1-z^2)^2\) & permutations
\(x^2 + x^2y^2 + y^2 = 1\), etc.

Obtuse Triangles
\(\mathbb{P}(\text{obtuse})=\frac{1}{4\pi}\text{Area} = \frac{24}{4\pi} \int_R d\theta dz\)


But now \(C\) has the parametrization
And the integral reduces to
Solution to the Pillow Problem
By Stokes’ Theorem

\(\frac{6}{\pi} \int_R d\theta dz=\frac{6}{\pi}\int_{\partial R}z d\theta = \frac{6}{\pi}\left(\int_{z=0} zd\theta + \int_C zd\theta \right)\)
\(\left(\sqrt{\frac{1-y^2}{1+y^2}},y,y\sqrt{\frac{1-y^2}{1+y^2}}\right)\)
\(\frac{6}{\pi} \int_0^1 \left(\frac{2y}{1+y^4}-\frac{y}{1+y^2}\right)dy\)
Our Answer
Theorem [w/ Cantarella, Needham, Stewart]
With respect to the symmetric measure on triangles, the probability that a random triangle is obtuse is
\(\frac{3}{2}-\frac{3\ln 2}{\pi}\approx0.838\)
Generalization
For \(n>3\), the sidelengths do not uniquely determine an \(n\)-gon, so the simplex approach doesn‘t obviously generalize.
Key Observation: The coordinates \((x,y,z)\) of a point on the sphere are the Plücker coordinates of the perpendicular 2-plane.
\(\vec{p}=\vec{a} \times \vec{b}\)
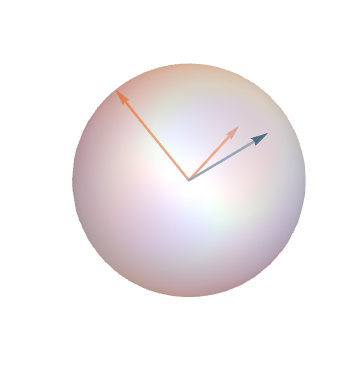
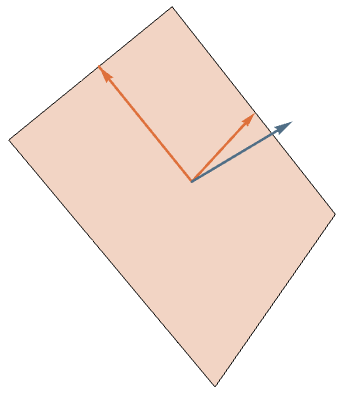
Planes and Polygons
In general, we can identify the collection of planar \(n\)-gons with \(G_2(\mathbb{R}^n)\), the Grassmannian of 2-planes through the origin in \(\mathbb{R}^n\).
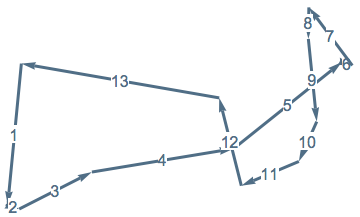
Definition [w/ Cantarella & Deguchi]
The symmetric measure on \(n\)-gons of perimeter 2 up to translation and rotation is the pushforward of Haar measure on \(G_2(\mathbb{R}^n)\).
Sylvester’s Four Point Problem
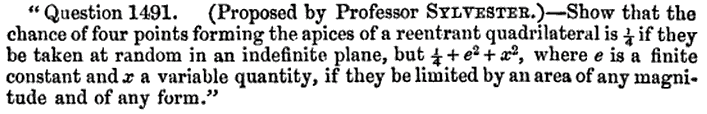

convex
reflex/reentrant
self-intersecting
Modern Reformulation: What is the probability that all vertices of a random quadrilateral lie on its convex hull?
Some Answers
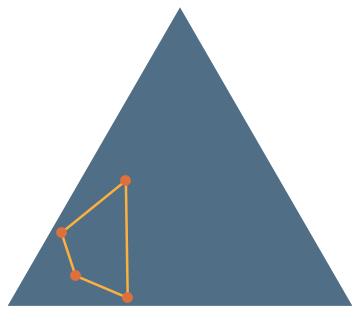
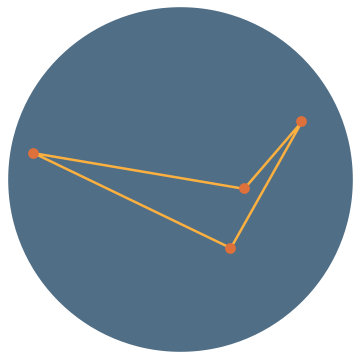
\(\mathbb{P}(\text{reflex})=\frac{1}{3}\)
\(\mathbb{P}(\text{reflex})=\frac{35}{12\pi^2}\approx 0.296\)
Theorem [Blaschke]

\(\frac{35}{12\pi^2}\leq\mathbb{P}(\text{reflex})\leq\frac{1}{3}\)
Our Answer
Theorem [w/ Cantarella, Needham, Stewart]
With respect to the symmetric measure, each of the three classes of quadrilaterals occurs with equal probability. In particular, \(\mathbb{P}(\text{reflex})=\frac{1}{3}\).
More generally...
Theorem [w/ Cantarella, Needham, Stewart]
With respect to any permutation-invariant measure on \(n\)-gon space, the probability that a random \(n\)-gon is convex is \(\frac{2}{(n-1)!}\).
A Question of Distances
What’s the shortest path from
to
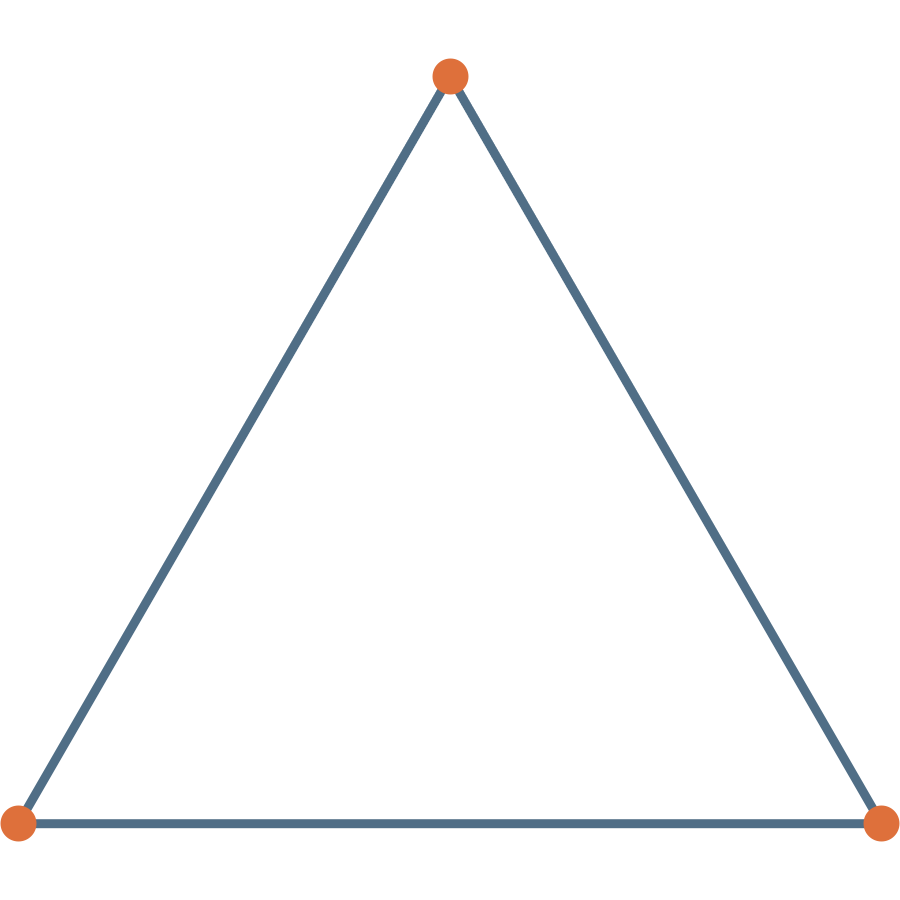
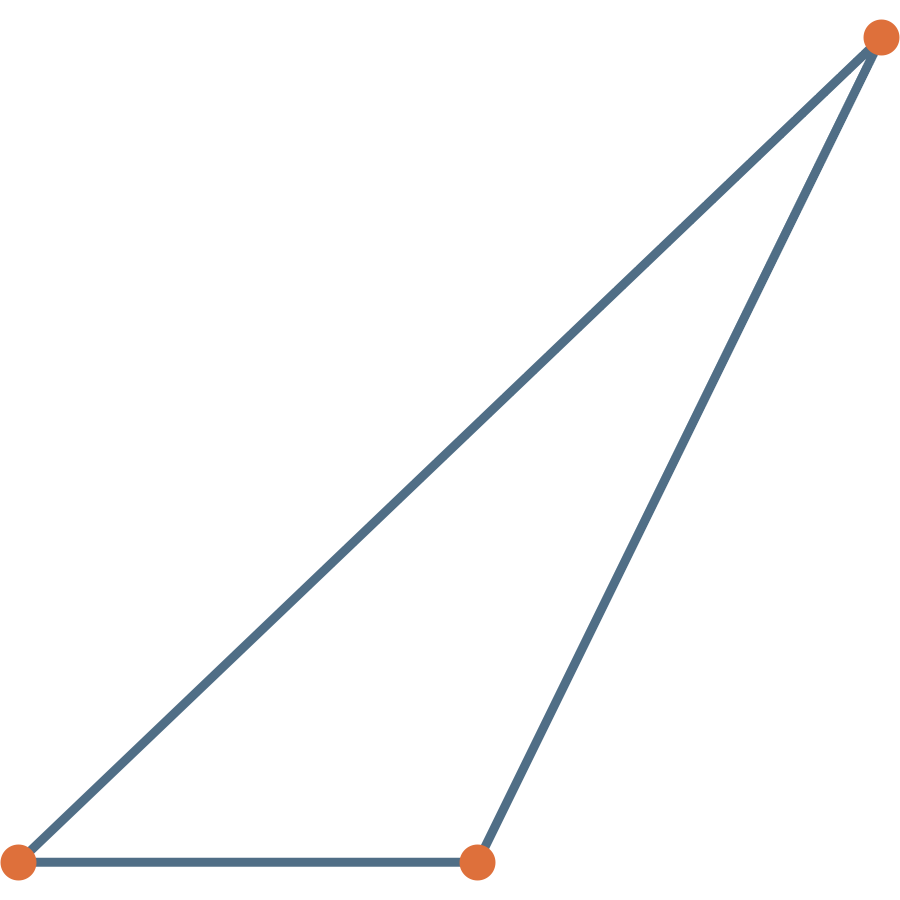
?




Shortest Paths Between Planes are Easy!


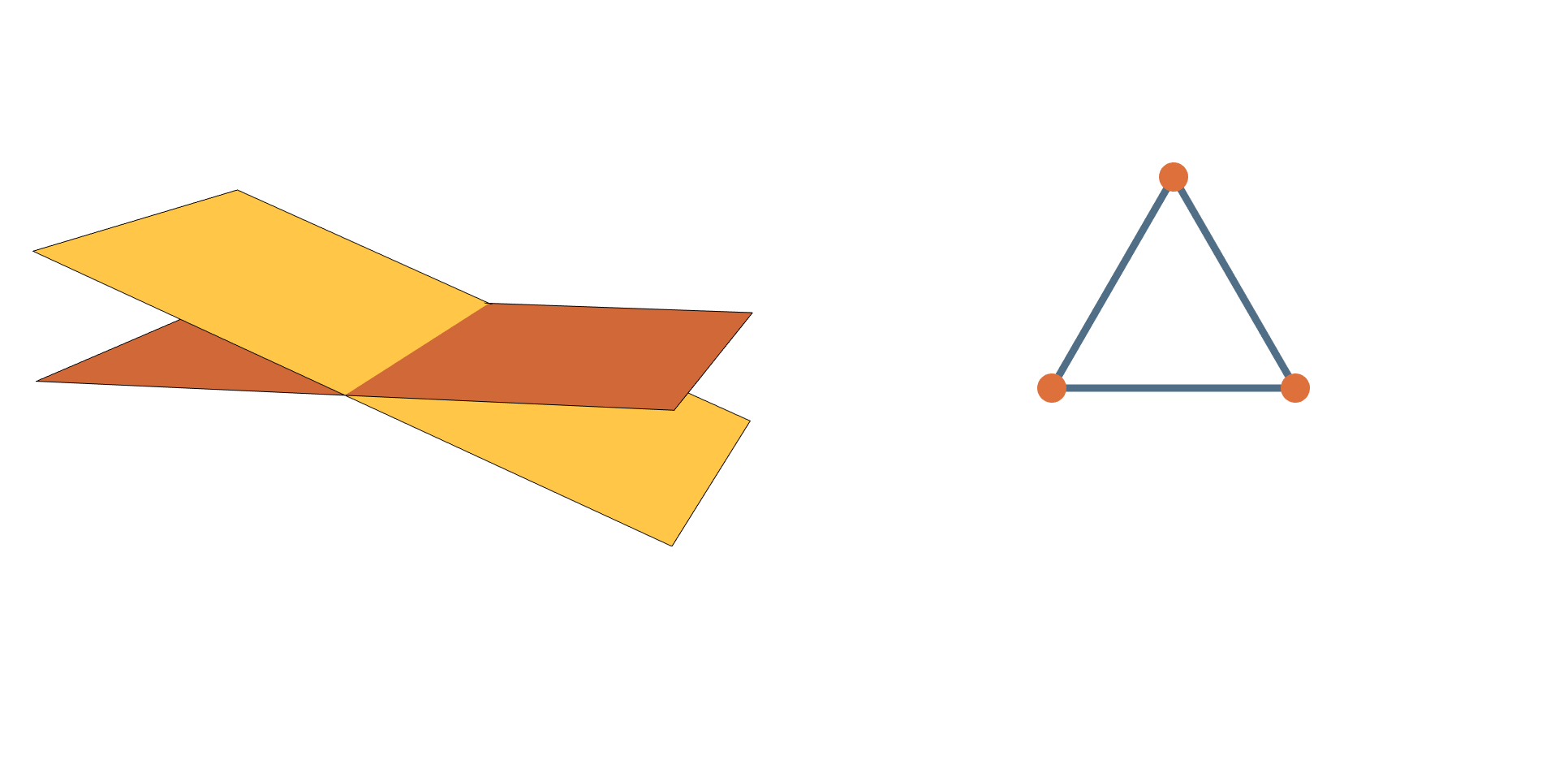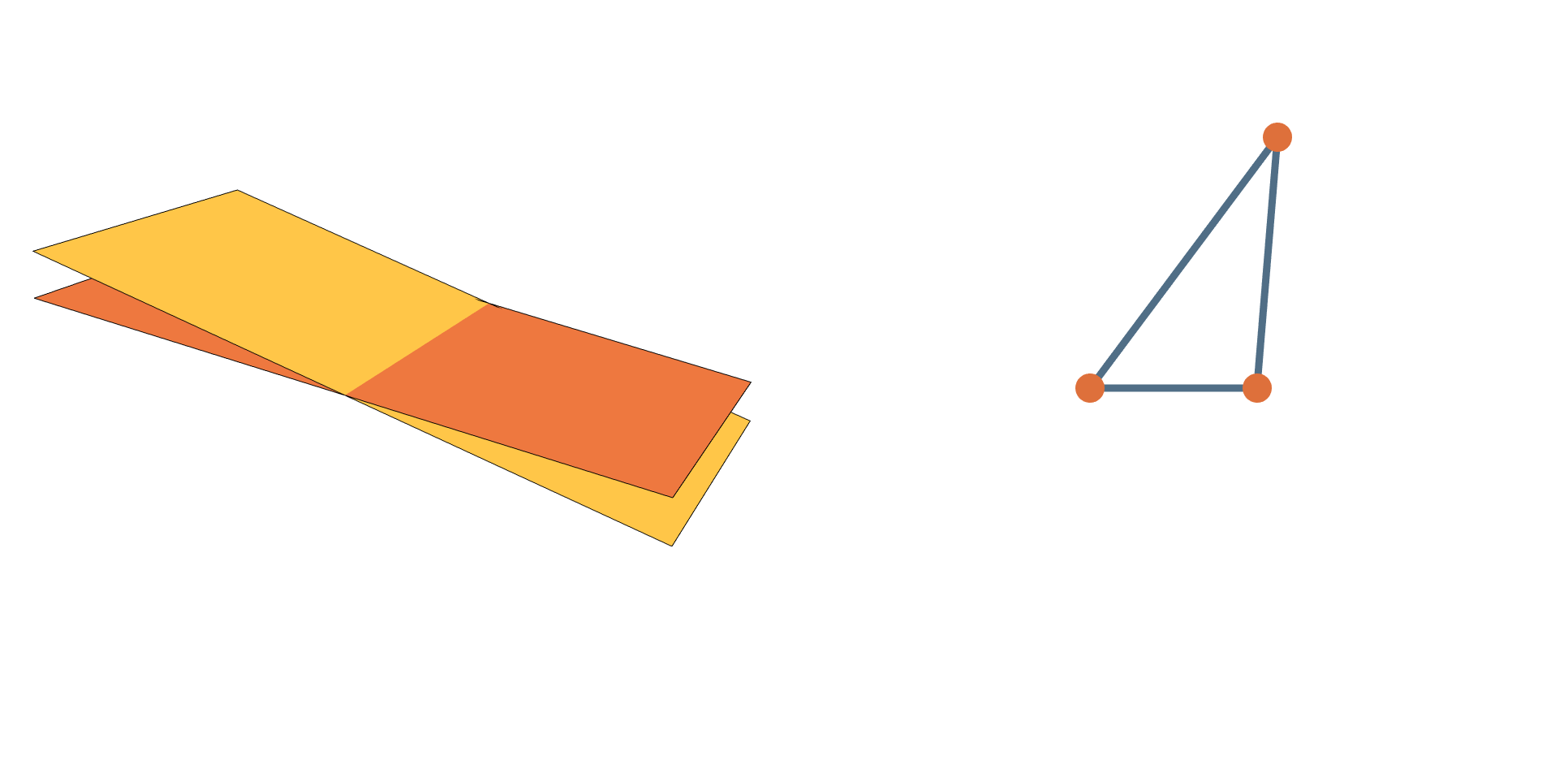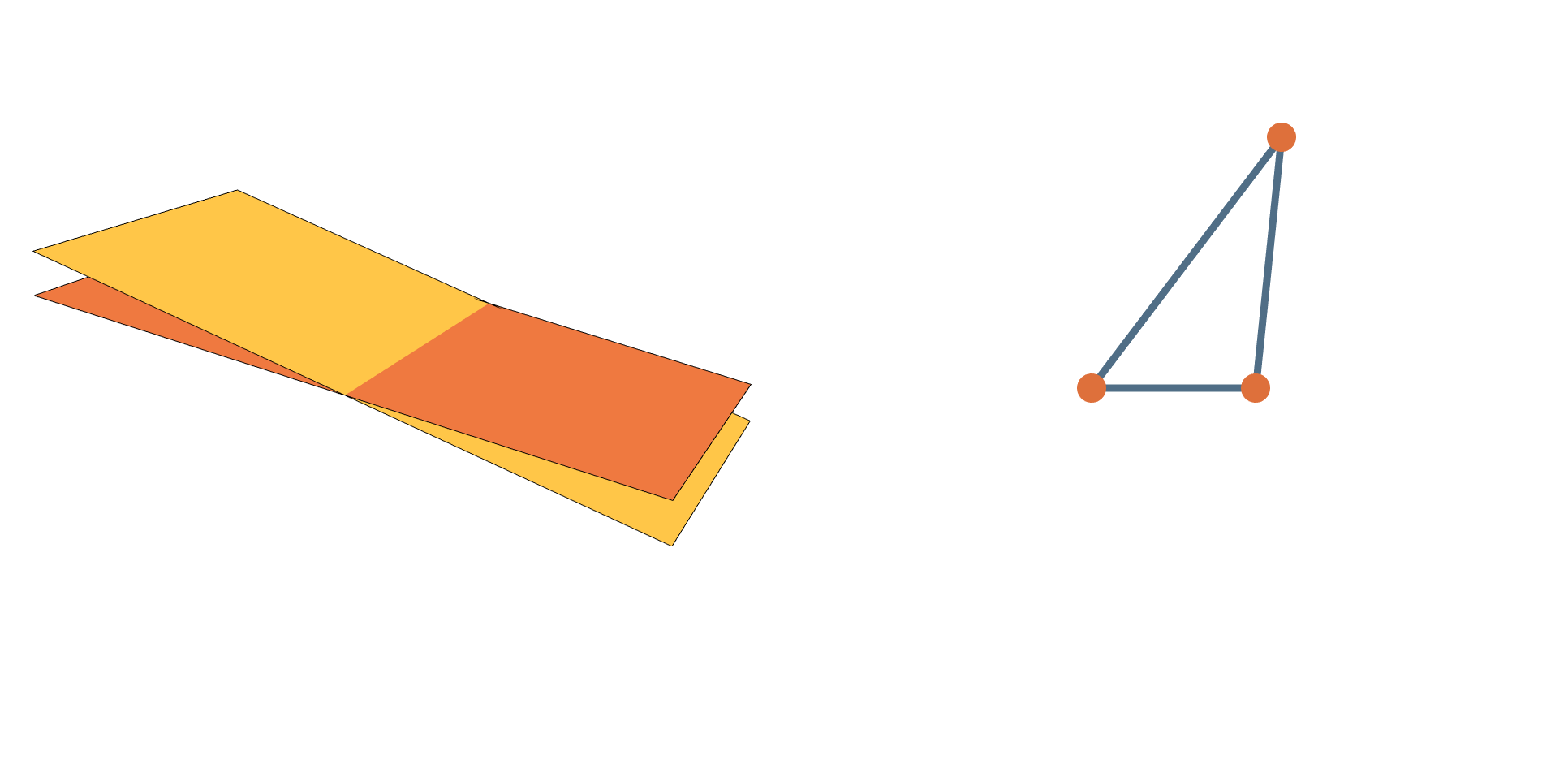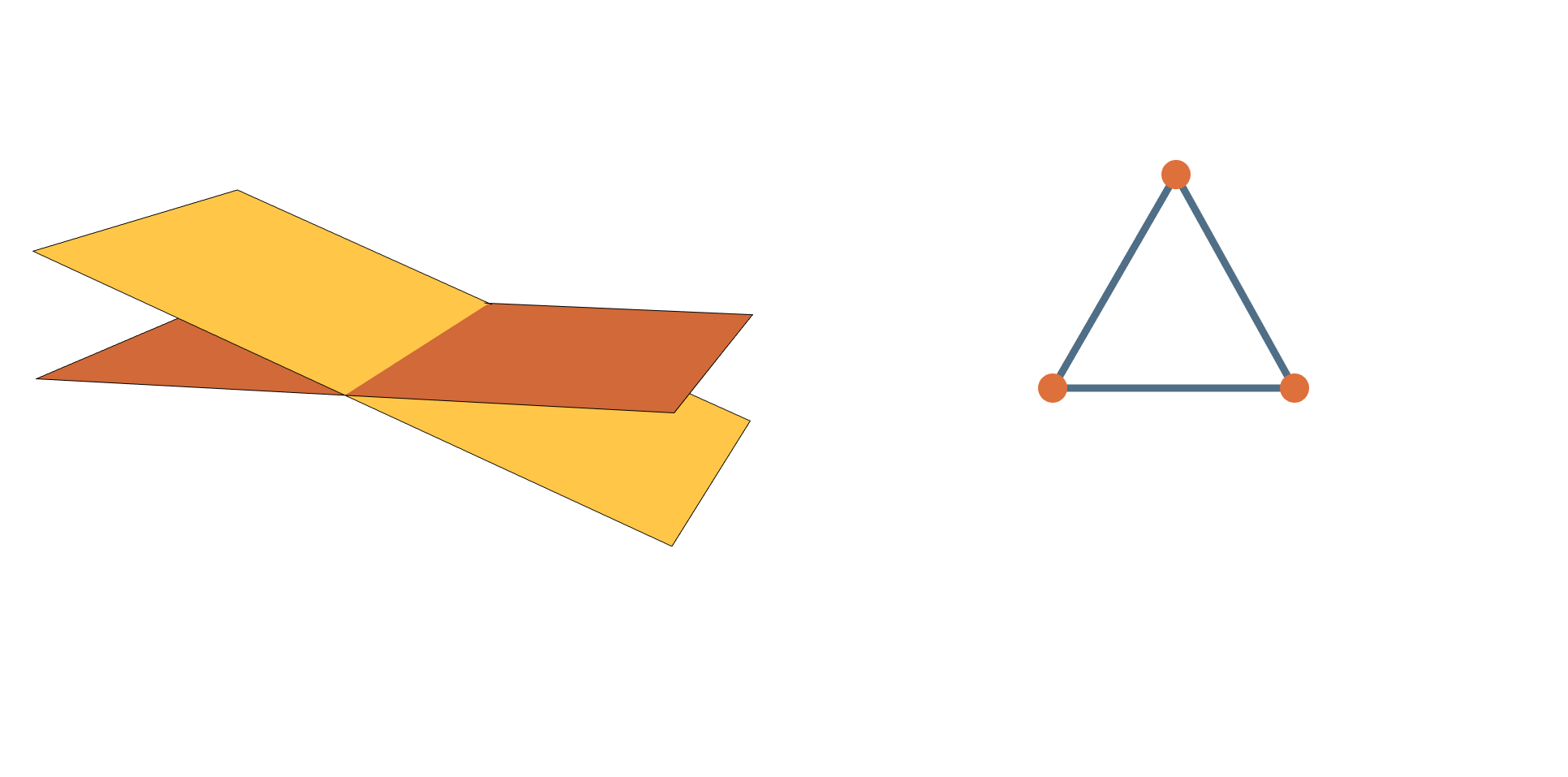
?
to
What’s the shortest path from




An Invariant Representation
Key Feature: This is a representation of \(n\)-gons which is invariant under translations and rotations, so we get the same distance and the same path whether our starting point is

or
Applications to shape recognition, medical imaging, etc.
Polygons in Space
There is a version of this story for \(n\)-gons in space as well.
Polygons in space provide a foundational theoretical and computational model for ring polymers like bacterial DNA.
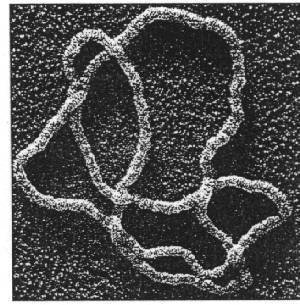

Wassermann et al., Science 229, 171--174

Lyubchenko, Micron 42, 196--206

Complex Grassmannians and Space Polygons
Polygons in space correspond to planes in complex \(n\)-dimensional space \(\mathbb{C}^n\), where again we understand distances and shortest paths very well.

to

?
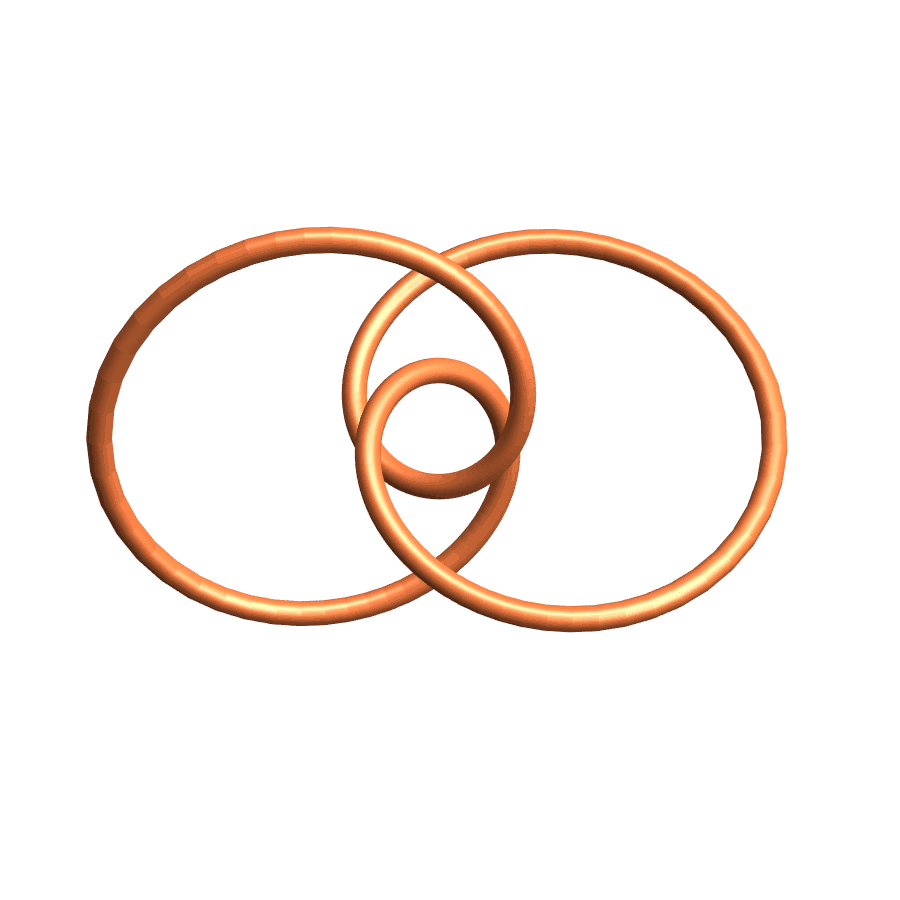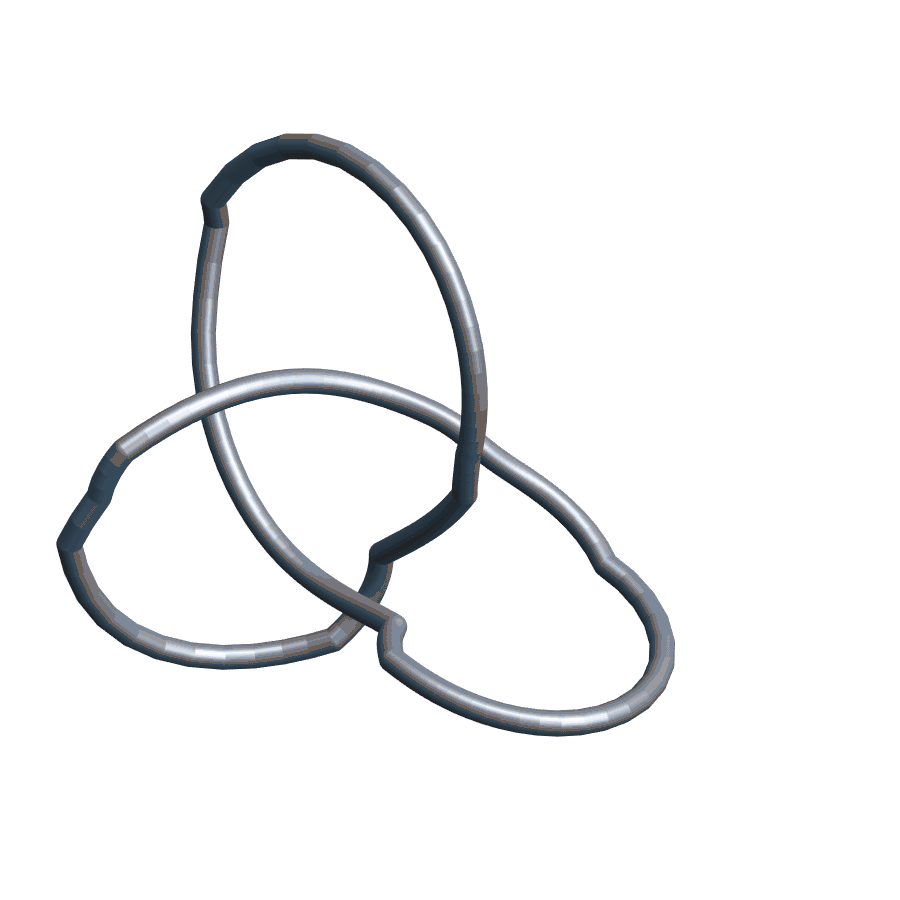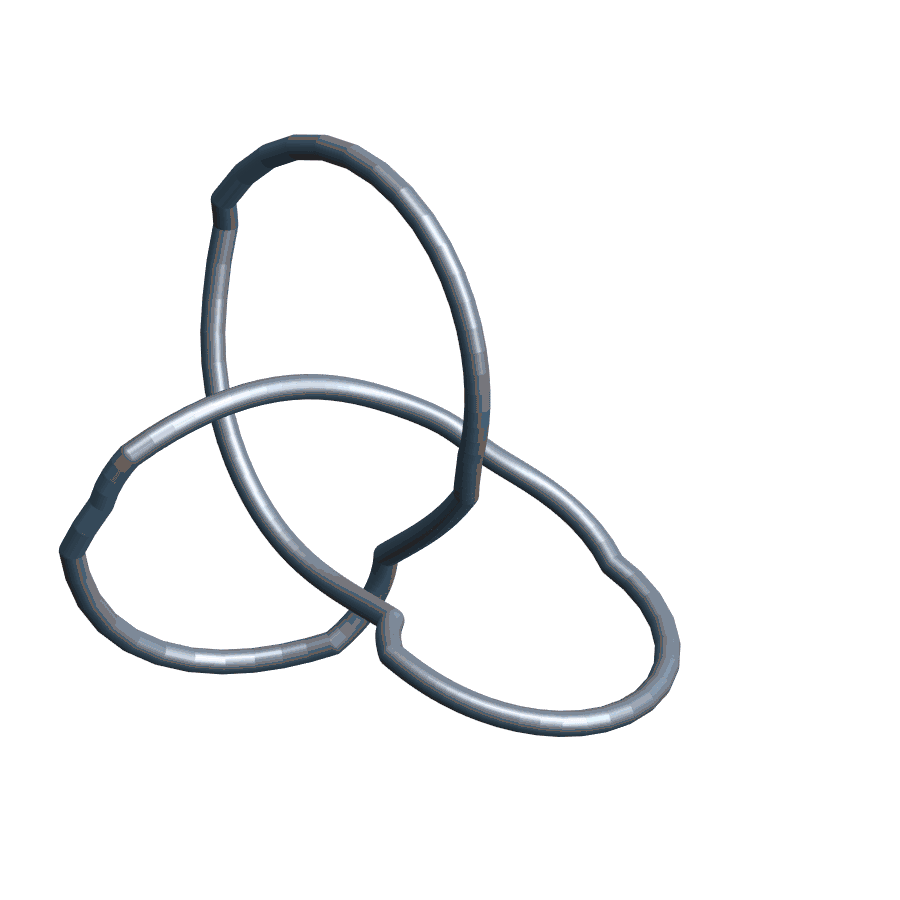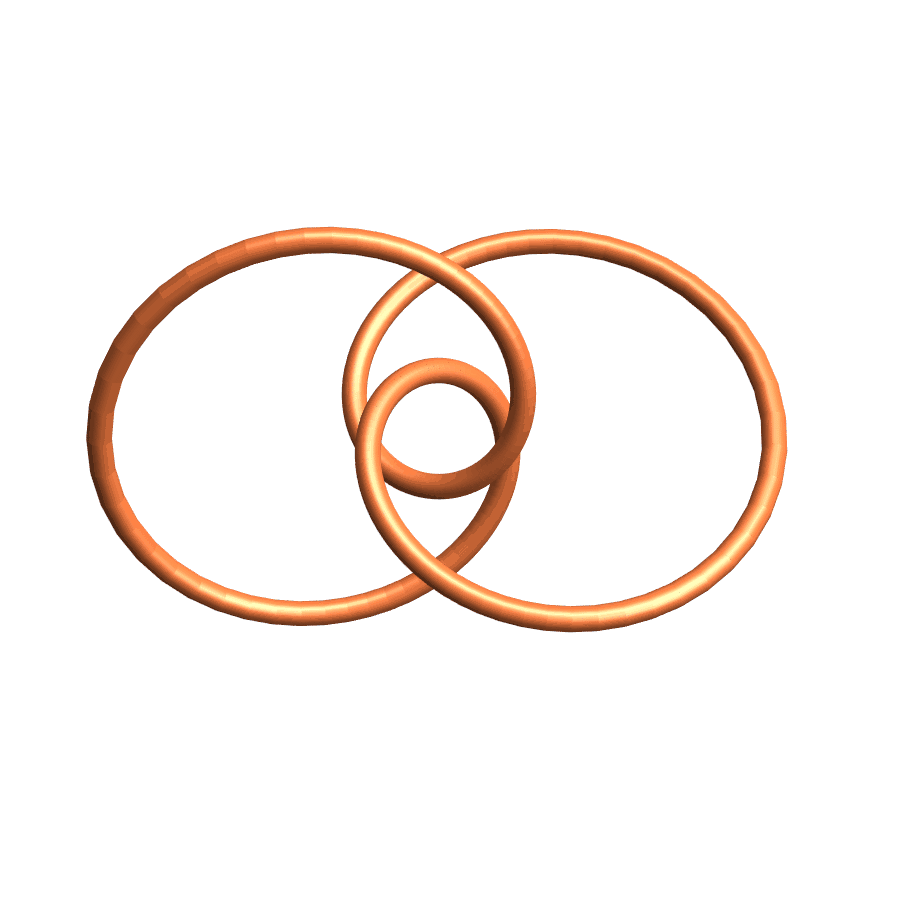
Again, Invariance
This representation of polygons is orientation-independent...
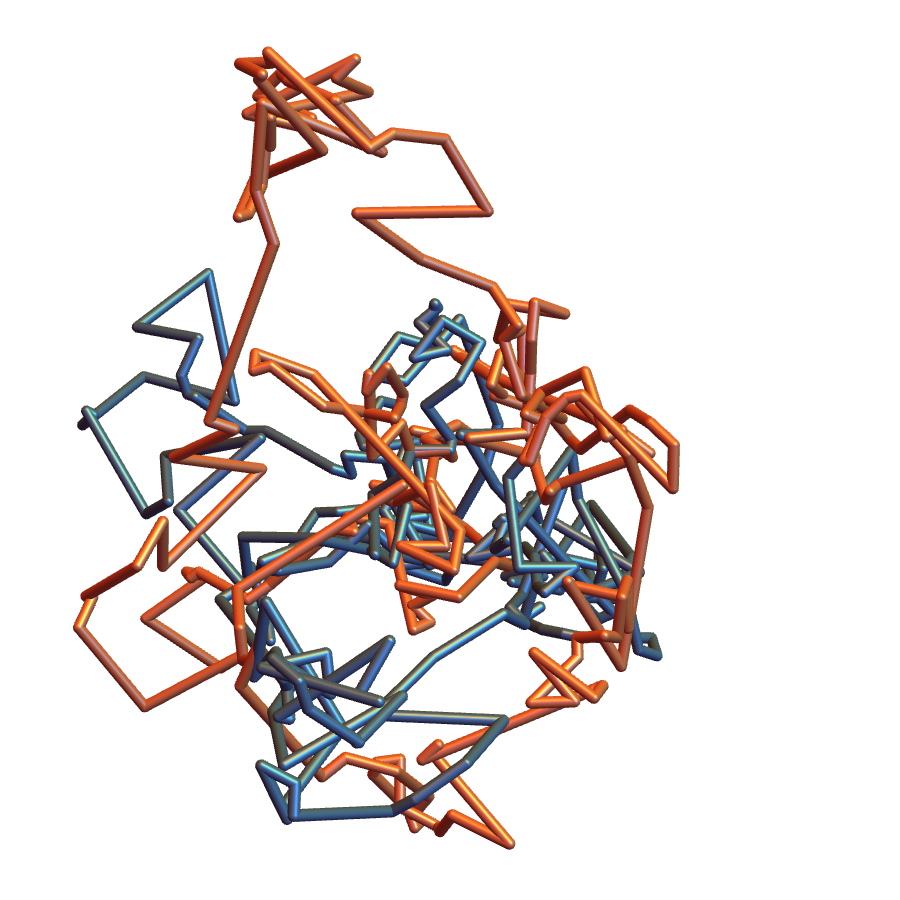
...so it’s easy to recognize these are the same shape and register them.
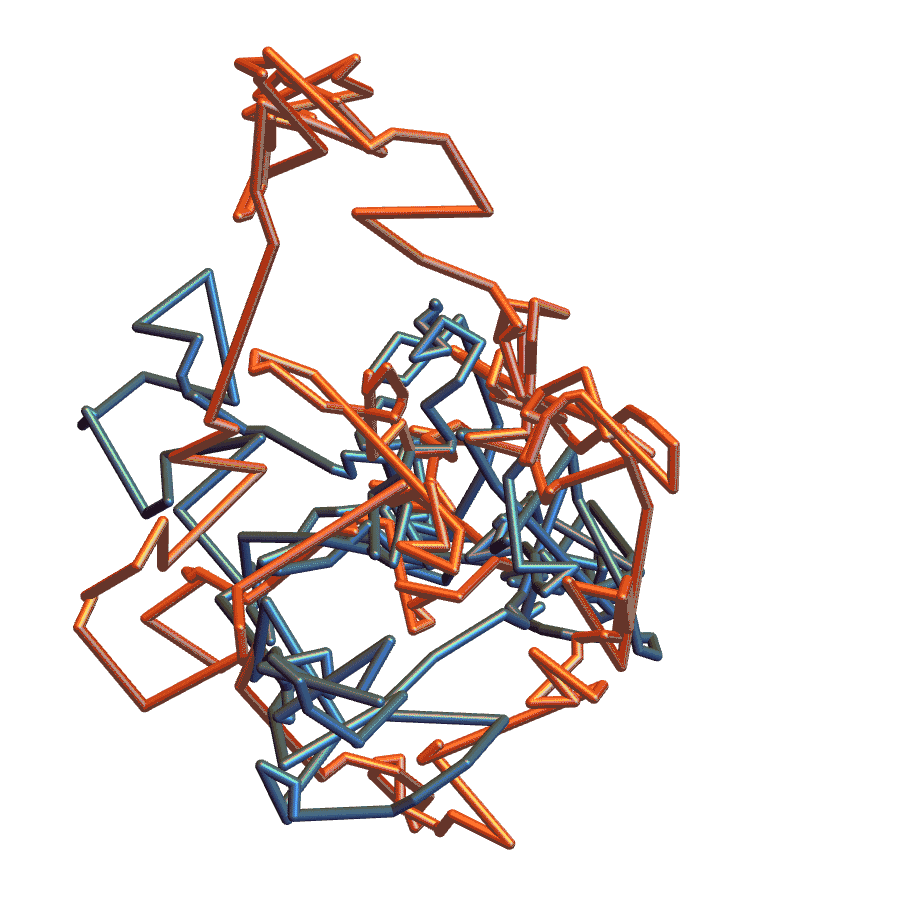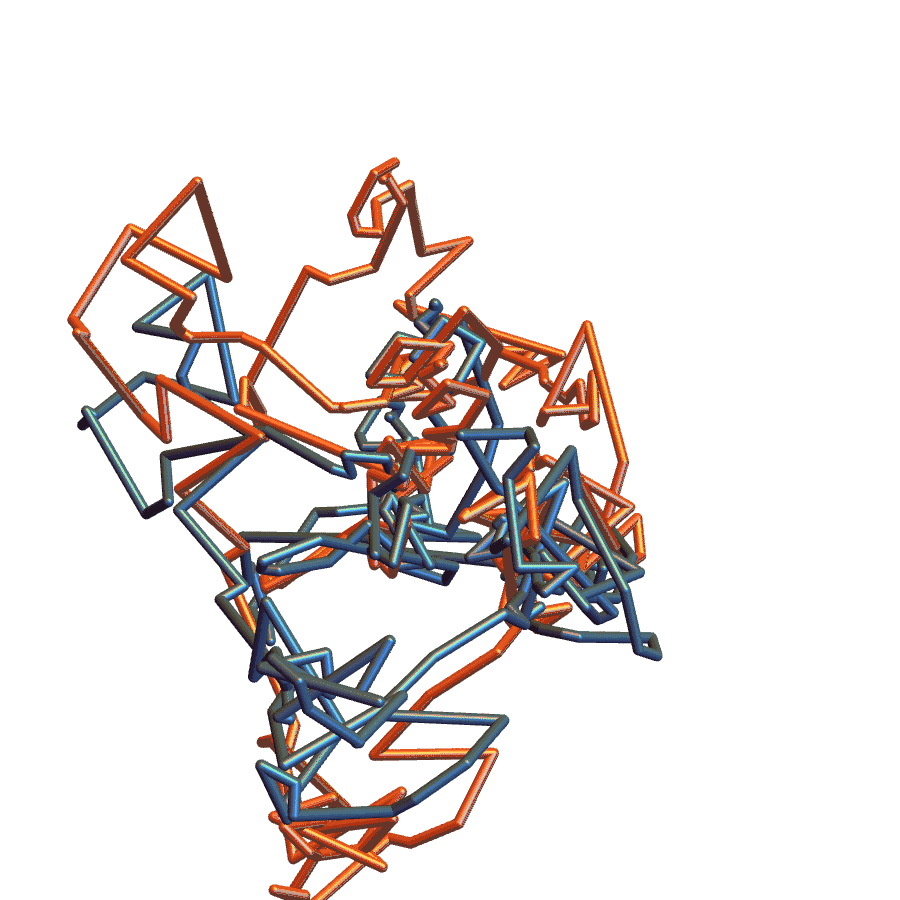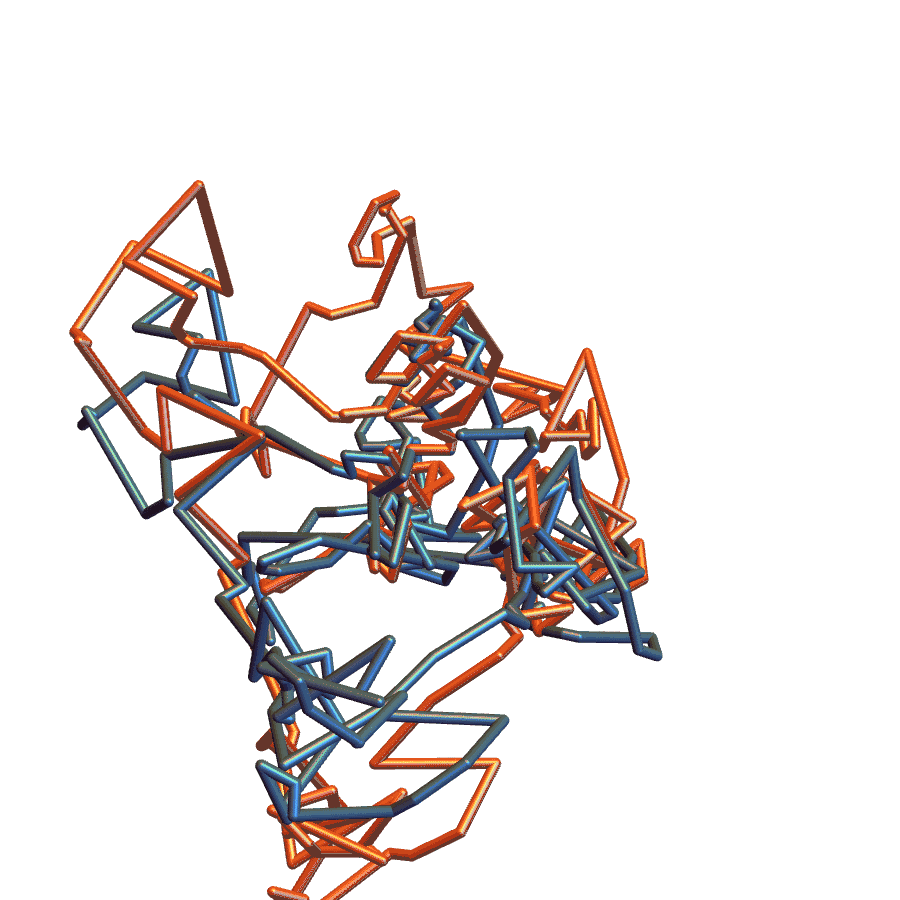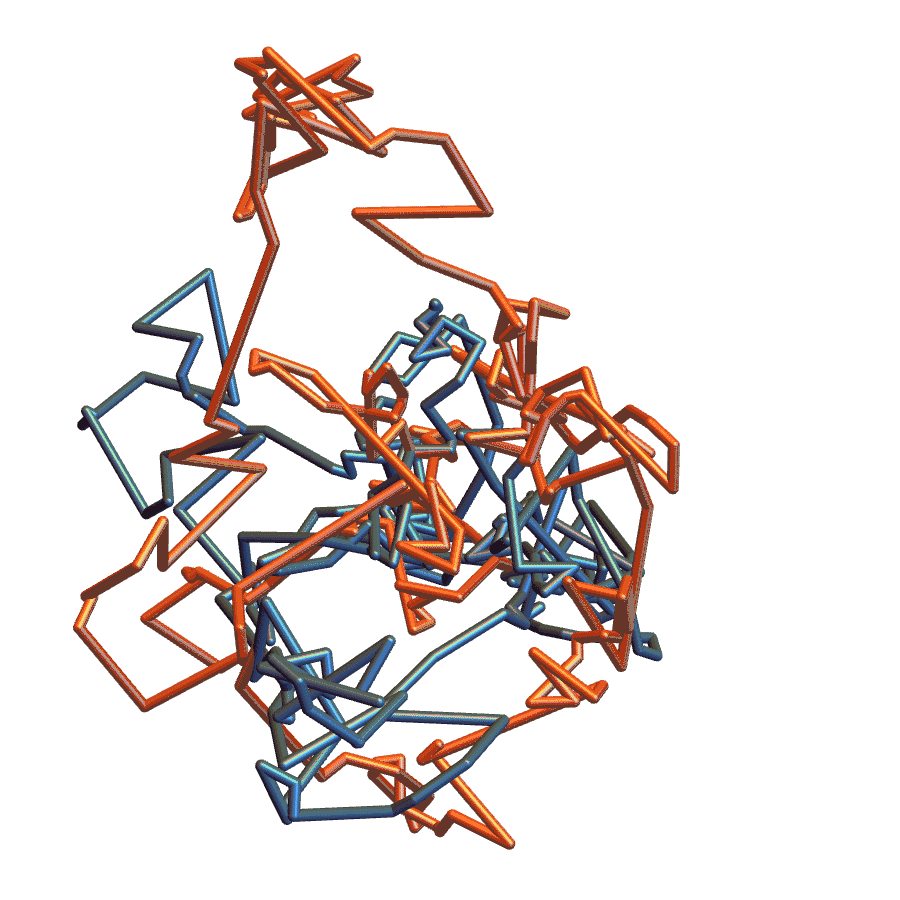
Application to Protein Clustering
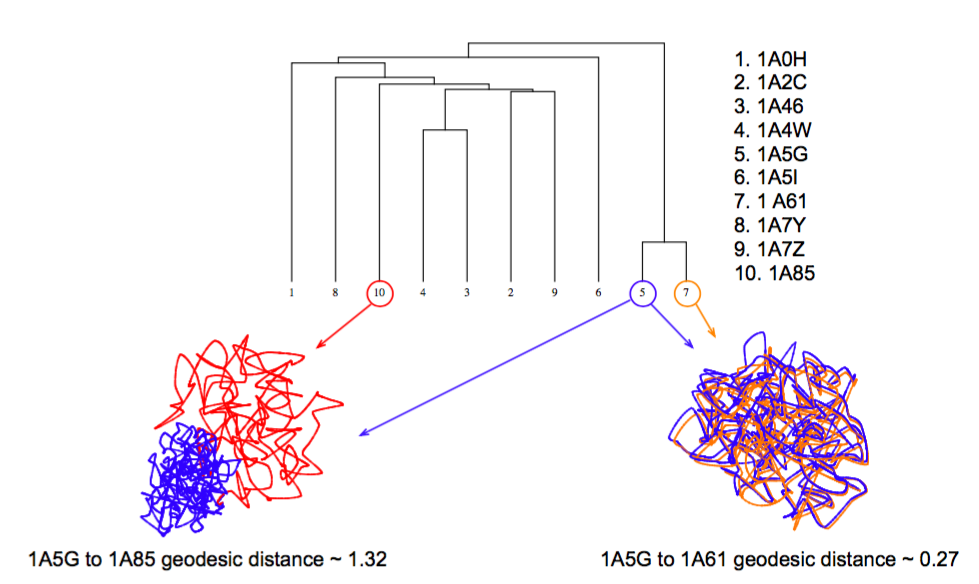
Needham, 2016
The Grassmannian perspective gives a way to
- Register 3-D loops
- Compute distances between 3-D loops
The challenge for the future is to compute distances and find shortest paths while avoiding self-intersection.
Many antibiotics (e.g., Cipro) and many anti-cancer drugs (especially for treating pediatric cancers; e.g. Etoposide) are topoisomerase inhibitors, which seem to work by preventing DNA from unknotting.
Challenge I
Why Does This Matter?
Challenge II
The Grassmannian theory deals with random polygonal loops; find the analogous theory for more complicated polygonal graphs.
Why Does This Matter?
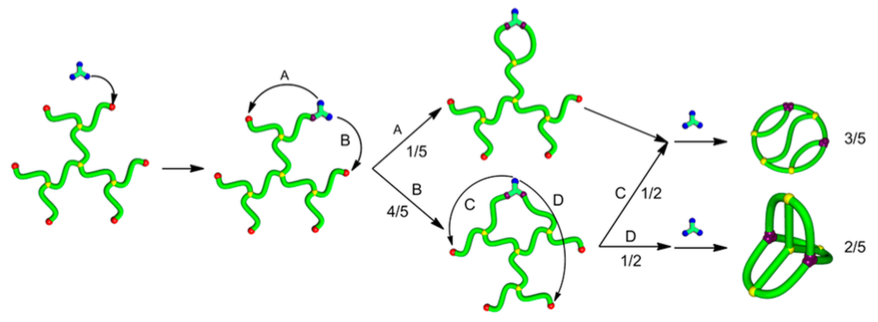
A synthetic \(K_{3,3}\) (Tezuka Lab, Tokyo)
Novel polymer topologies have novel material properties.
More geodesics in polygon space





Thank you!
Square Roots of Angles
It turns out that if we take square roots of angles instead, we get:
\(\mathbb{P}(\text{obtuse}) = \frac{4-2\sqrt{2}}{\sqrt{\pi}} \approx 0.661\)
But this approach doesn’t seem to generalize nearly as well as taking square roots of edgelengths.
