Steepest Descent Method

In the linear system Ax = b suppose the coefficient matrix A is symmetric and positive definite. Solving Ax = b is equivalent to minimizing the quadratic function $Q(x) = {1\over 2} x^{T}Ax - x^{T}b$.

Example: The following linear system of the form Ax = b arises in connection with the Laplace Finite Difference equation on a 3x3 square grid.

$$\left[ \begin{array} {*{9}{r}} 4_{\ }&-1& 0&-1& 0& 0& 0& 0&... ...5 \\ b_6 \\ b_6 \\ b_7 \\ b_8 \\ b_9 \\ \end{array}\right]$$

For this example, the function Q(x) is given by

$$Q(x) = {1\over 2} \sum^{9}_{i,j=1}x_{i} a_{ij} x_{j} - \sum^{9}_{i=1}x_{i}b_{i} .$$

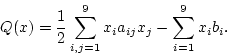
From calculus, we know that if Q(x) has a minimum at some point x, then all the partial derivatives of Q must be zero at that point. Calculating the partial derivatives of Q with respect to each x_i, and setting each partial derivative to zero results in the linear system Ax - b = 0 or Ax = b. From this we see that it is correct to view Ax - b as the gradient of Q and write $\nabla Q(x) = Ax - b$.

In the method of steepest descent, we make an initial estimate of the solution x to Ax = b and then proceed down gradients of Q to arrive at the minimum of Q and thus arrive at the solution to Ax = b. In this connection, define the residual rⁱ associated with the approximate x ⁱ to be

$$r^{i} = b - Ax^{i} = -\nabla Q(x^{i})$$

We define our next estimate to the solution of Ax = b to be down gradient of xⁱ by setting

$$x^{i+1} = x^{i} + \alpha _{i}r^{i}.$$

Now it remains to pick a value of $\alpha_{i}$ that determines how far we go in the down gradient direction defined by rⁱ. We choose $\alpha_{i}$ so that we minimize

$$F(\alpha ) = Q(x^{i} + \alpha r^{i}).$$

The rest of the steepest descent method follows from calculus: find $F'(\alpha )$ and set $F'(\alpha ) = 0.$ By the chain rule,

$$F'(\alpha ) = \nabla Q(x^{i} + \alpha r^{i})\cdot r^{i}$$

$$= \left[\matrix{A(x^{i}&+&\alpha r^{i})&-&b}\right]\cdot r^{i}$$

$$= \left[\matrix{ Ax^{i}&+&\alpha Ar^{i}&-&b}\right]\cdot r^{i}$$

$$= \left[\matrix{-r^{i}&+&\alpha Ar^{i}}\right]\cdot r^{i}$$

By setting $F'(\alpha ) = 0$,we can see that $\alpha_{i}$ for computing xⁱ⁺¹ is given by

$$\alpha_{i} = {r^{i}\cdot r^{i}\over r^{i}\cdot Ar^{i}}$$

The method of steepest descent is easy to program, but it often converges slowly. The main reason for its slow convergence is that the method may spend time minimizing Q along parallel or nearly parallel search directions.