Return to Applet

In this applet we illustrate the Jacobi iterative method for approximating the solution to a system of linear equations. We apply the Jacobi method to the Laplace finite difference equation

$$U_{m-1,n}+U_{m,n-1}-4U_{mn}+U_{m+1,n}+U_{m,n+1}=0\;\;for\;m,n=1,2,...50$$

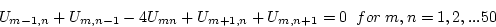
with boundary conditions given by

$$U_{0,n}=U_{m,0}=100 \;\;for\;m,n=1,2,...50$$

$$U_{51,n}=U_{m,51}=0 \;\;for\;m,n=1,2,...50$$

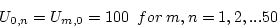
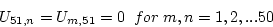
The Laplace difference equation is equivalent to the discrete mean value property

U_mn=.25*(U_m-1,n+U_m,n-1+U_m+1,n+U_m,n+1)

which states that the solution value at (m,n) is the average of the solution values at the four compass-point neighbor grid points.

The mean value property motivates a method for solving the system of difference equations. Let us make an initial guess of the interior solution values of

$$U_{mn}^{0} = 50 \;\;for\;m,n=1,2,...50$$

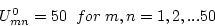
We have chosen the initial guess on the interior to be the average of the boundary values. Next, successively apply the discrete mean value property with the aim of improving our initial guess. The Jacobi iterative method applied to this problem calls for successive estimates of U_mnⁱ to be computed from

$$U_{mn}^{i+1}=.25*(U_{m-1,n}^i+U_{m,n-1}^i+U_{m+1,n}^i+U_{m,n+1}^i)\;\;for\;m,n=1,2,...50$$

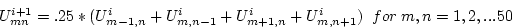
iterating on i until the maximal residual value given by the maximum over m,n = 1,2,...,50 of

$$\left\vert(U_{m-1,n}^i+U_{m,n-1}^i-4U_{mn}^{i}+U_{m+1,n}^i+U_{m,n+1}^i)\right\vert$$

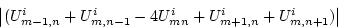
is less than some user prescribed tolerance.