Return to Applet
This applet simulates the flow of a DNAPL (Dense Nonaqueous Phase Liquid)
into an initially water saturated porous medium. Initally, the DNAPL is
confined to the upper left quarter of the vertical cross section. At time
t = 0, the DNAPL is released and is free to infiltrate the water saturated
region. The mathematical model is based on Darcy's law and conservation
of mass. Darcy's law asserts that the mass flux of each fluid is given by
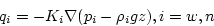
where i = w denotes the wetting fluid (water) and i = n denotes the
nonwetting DNAPL. In Darcy's law, g is the gravitational constant,
z is the vertical distance from the top of the flow region and the
proportionality factor Ki is the hydraulic conductivity of the
phase-i fluid. Let Si denote the relative saturation of phase-i
fluid and 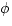 the porosity of the porous medium. Then conservation
of mass implies
the porosity of the porous medium. Then conservation
of mass implies
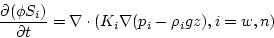
To complete the mathematical model, we introduce the capillary pressure
pc = pn - pw
and assume constitutive relationships of the form:
Sw = F(pc)
Sn = 1 - Sw
Ki = Gi(Si)
For physical reasons, F'(pc) < 0 where 0 < Sw < 1 and 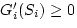 for i = w,n.
This leads to model equations of the form
for i = w,n.
This leads to model equations of the form
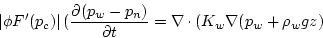
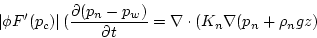
Return to Applet
About this document ...
Dave Zachmann
3/10/1999
![]()
![]()
![]()
![]()