Math 670: Introduction to Differentiable Manifolds
|
|
WHEN: MWF 11 – 11:50 am
WHERE: WEBER 223 // in the oval with good weather
WHAT: A graduate level introduction to the theory of
differentiable manifolds.
TEXTBOOK: Introduction
to Smooth Manifolds (John
M. Lee)
|
|
Since our wee years as budding mathematicians
we have been fond and comfortable with euclidean spaces, i.e. spaces that can be
coordinatized by n-tuples of real
numbers and metrized using the Pythagorean theorem. We learned to study
functions from euclidean spaces to euclidean spaces, and do all sort of fancy
stuff such as differentiating and integrating. If we stop and ponder, however,
we soon realize that to take a derivative, we don’t need the whole
universe to be euclidean, but only a little open neighborhood od the point we
want to take the derivative of. Integration is a global operation, but it is
obtained by “adding up infinitely many infinitesimal things” (oh gods of math forgive my sloppiness)
that are also constructed locally.
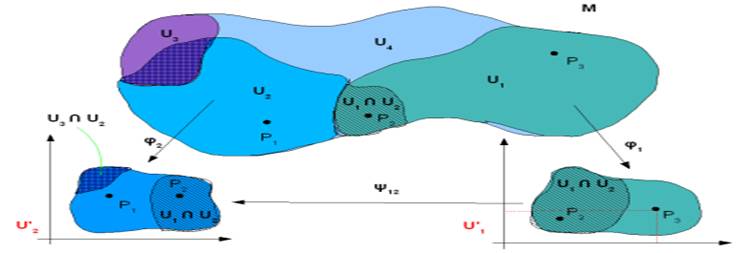
Therefore any space that can be
locally (and appropriately) identified with euclidean space is suitable for
integration and differentiation.
This is the basic insight that starts the
theory of differentiable manifolds. Manifolds are precisely spaces that are
“locally euclidean” but not necessarily globally so. Think this is
a funky idea? Well if you think about it we live on a differentiable manifold,
and we look at a collection of euclidean identifications of it everytime we
flip through pages of the AAA Road Map of the US. So needless to say I think
this is an extremely natural and foundational theory to just about all of
mathematics (yes, even you purist of algebra and you applied mathematician
should care about manifolds!)
The focus of this class will be on getting a
basic overview of many features of the theory, introducing manifolds, bundles,
vector fields and differential forms. We will prove some interesting
non-trivial theorems, such as the Whitney embedding theorem. And we’ll at
least introduce some interesting examples of manifolds, such as Lie Groups and
manipulations thereof (such as Projective Spaces and Grassmannians). I am planning
on covering good part of the first 10 chapters of the textbook. My guess is
that this will already keep us entertained for most of the semester.
HOMEWORK: Yes, there will be homework. Not much, but hopefully steady. Not
necessarily graded, but probably collected. All sort of flexibility can be
worked out, but in order to really make things sink in we should really make a
(collective) effort to keep up with it.
|
DATE DUE: |
|
|
Jan 28th |
1) Exercises 1.1, 1.3 page 21. |
|
Feb 4th |
Let
f(x,y) and g(x,y) be two polynomials in two variables. By setting z
= f(x,y) w
= g(x,y) we get a smooth function from the
plane (with coordinates x,y) to the plane (with
coordinates z,w). What
are the conditions on f and g for this function to descend to a smooth
function from the projective line to the projective line? Can
you generalize this construction to more than two variables and give an
example of a smooth function from P^3 to P^5? |
|
Feb 11th |
Exercises
3-1, page 64. |
|
Feb 18th |
Exercises
3-4, 3-5 page 64. |
|
Feb 25th |
Prove that the following conditions are
equivalent: 1) V is a smooth vector field on X 2) Every component of every local
representation of V is a smooth function. 3) For every smooth function f: X->IR , the function Vf : X-> IR
is smooth. |
|
Mar 4th |
Exercise 4.1, page 90 |
|
Mar 11th |
Exercises 5-1, 5-5,
5-18 pages 126, 128 |
|
Apr 8th |
Exercises 6-4,6-5 page 144 |
|
May 6th |
Compute the de Rham cohomology vecor spaces of: ·
The
n-dimensional sphere. ·
Real
projective plane. ·
The
figure eight. ·
The
union at a point of two manifolds. For the last two spaces, what we intend is “some manifold
which is homotopy equivalent to…” but
you can use the singular space in your constructions. |
|
|
|
|
|
|
|
|
|
|
|
|