Applied and Computational Topology
.png)


Universidad de Costa Rica, Summer 2017


Instructors: Henry Adams and Joshua Mirth
Email: henry dot adams at colostate dot edu and mirth at math dot colostate dot edu
Class: June 27 - July 6, 2017
Overview: This class is an introduction to applied and computational topology. We will first give an intuitive introduction to topology, including homotopy equivalent spaces, homology groups, and homotopy groups. We next move to the realm of data analysis: given only a dataset, i.e. a finite sampling from a space, what can we say about the space's shape (which may be reflective of patterns within the data)? The main technique we cover is persistent homology; we describe its theoretical underpinnings, discuss examples of how it has been used on real-life data, and provide coding examples. We also discuss zigzag homology and applications to mobile sensor networks.
Portions of our class will use the tutorial for computing persistent homology with the Javaplex software package.
Schedule
| Date | Topic | Remark |
| Tues, June 27, 7-10am | An introduction to applied and computational topology (Slides) | 4th floor room |
| Čech and Vietoris-Rips simplicial complexes | ||
| The nerve lemma and Latschev's theorem | ||
| Stability of persistent homology | ||
| Wed, June 28, 9am-12pm | Simplicial homology computations in Javaplex | 2nd floor computer lab |
| Exercises 1-2 in the tutorial | ||
| Persistent homology and Vietoris-Rips in Javaplex | ||
| Exercises 8-11 in the tutorial | ||
| Jung's theorem and Čech, Vietoris-Rips interleavings | ||
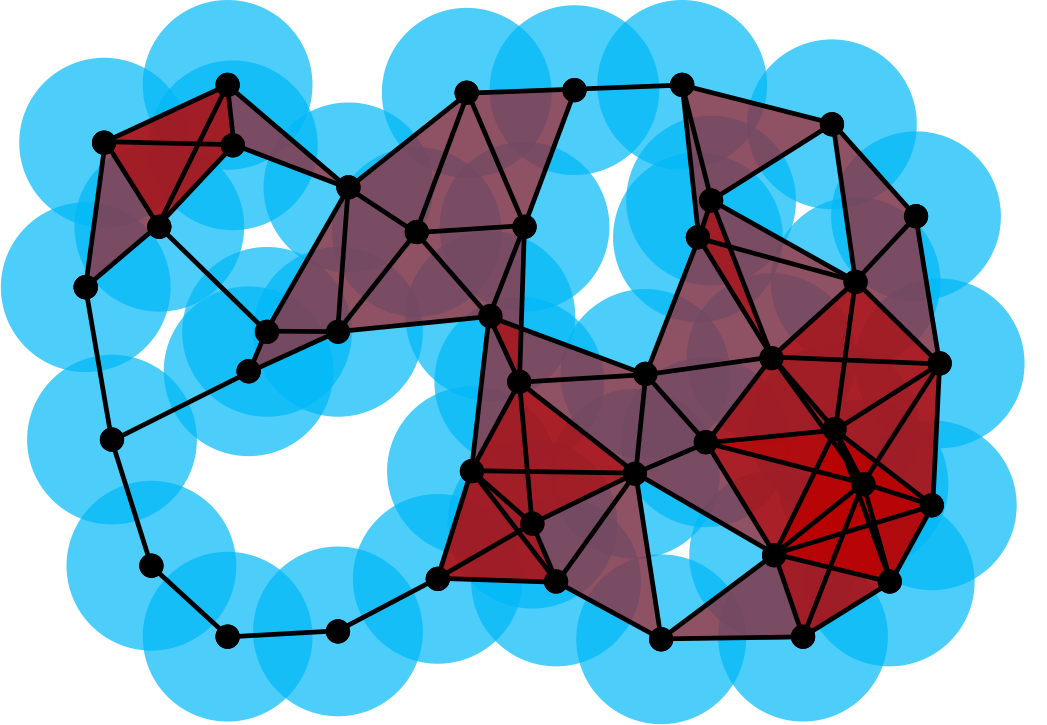
| Fri, June 30, 8am-10am | Voronoi diagrams and Delaunay triangulations | 4th floor room |
| Alpha complexes (and exercises) | ||
| Evasion paths in mobile sensor networks (Slides) | ||
| Mon, July 3, 4-7pm | Homology computations with different coefficients | 4th floor room |
| Torus and Klein bottle examples | ||
| An algorithm for persistent homology | ||
| Wed, July 5, 9am-12pm | Witness complexes & examples in Javaplex | 2nd floor computer lab |
| Torus and Klein bottle as identification spaces in Javaplex | ||
| Real datasets in Javaplex | ||
| Thurs, July 6, 4-6pm | Homology of the projective plane | 4th floor room |
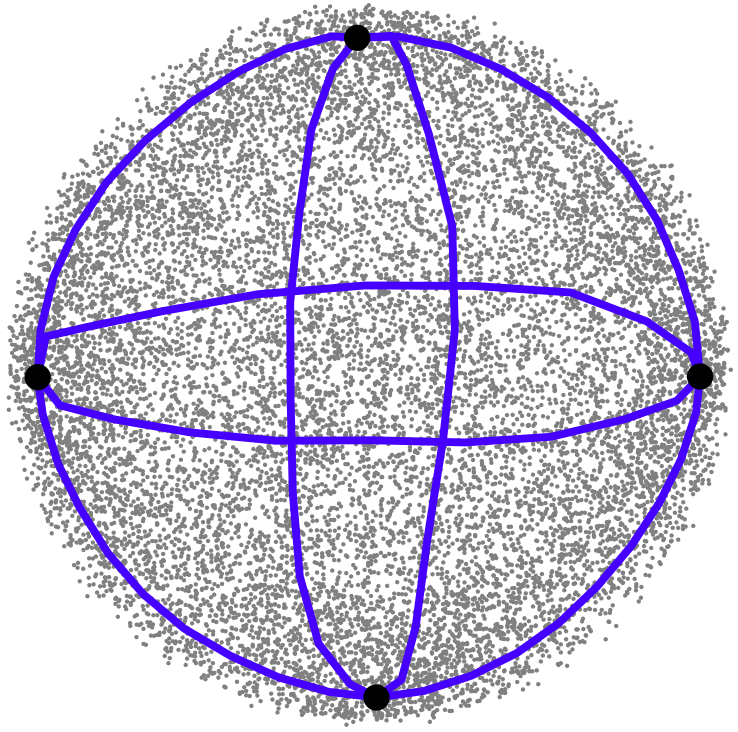
| Vietoris-Rips complexes of the circle (Slides) | ||
| Metric reconstruction via optimal transport (Notes, Paper) | ||
Other Notes
Notes on Čech and Vietoris-Rips complexesMathematica demo on Čech and Vietoris-Rips complexes
Mathematica demo on Vietoris-Rips and witness complexes
Mathematica demo on witness complexes
Installing Javaplex in Matlab
- Go to the GitHub webpage with the latest Javaplex release:
https://github.com/appliedtopology/javaplex/releases - Download "matlab-examples-4.3.1.zip" and "javaplex_tutorial.pdf"
- Unzip the folder "matlab-examples-4.3.1.zip"
- Paste the resulting folder "matlab-examples" into the Matlab directory (perhaps home/lab-217-##)
- >> cd matlab-examples
- >> load_javaplex
- >> import edu.stanford.math.plex4.*;
- >> cd tutorial_examples
- >> optical_image_example